
When it comes to the calculation of derivatives, there is a rule of thumb out there that goes something like this: either the function is basic, in which case we can appeal to the table of derivatives, or the function is composite, in which case we can differentiated it recursively — by breaking it down into the derivatives of its constituents via a series of derivative rules.
Indeed, for those of us who have ever read a calculus textbook or attended a calculus course, we might be already familiar with most — if not all — of these derivative rules:
If the function $cf$ is defined on an interval $I$ and $f$ is differentiable on $I$, then $\displaystyle (cf)’=cf’$ on $I$.
Given a real number $r$ greater or equal to $1$ , $(x^r)’ = r x^{r-1}$ for all $x \in \mathbb{R}$. In the case where $r$ is less than $1$ (and non-zero), $(x^r)’ = r x^{r-1}$ for all $x \ne 0$.
If the function $f+g$ is well-defined on an interval $I$, with $f$ and $g$ being both differentiable on $I$, then $\displaystyle (f+g)’ = f’ + g’$ on $I$.
If the function $f-g$ is well-defined on an interval $I$, with $f$ and $g$ being both differentiable on $I$, then $\displaystyle (f-g)’ = f’ – g’$ on $I$.
If the function $fg$ is well-defined on an interval $I$, with $f$ and $g$ being both differentiable on $I$, then $\displaystyle (fg)’ = f’g + fg’$ on $I$.
If the function $\displaystyle \frac{1}{f}$ is well-defined on an interval $I$, with $f$ being differentiable on $I$, then $\displaystyle \left( \frac{1}{f} \right)’ = \frac{-f’}{f^2}$ on $I$.
If the function $\displaystyle \frac{f}{g}$ is well-defined on an interval $I$, with $f$ and $g$ being both differentiable on $I$, then $\displaystyle \left( \frac{f}{g} \right)’ = \frac{f’g – fg’}{g^2}$ on $I$.
If the function $f \circ g$ in well-defined on an interval $I$, with $g$ being differentiable on $I$ and $f$ being differentiable on $g(I)$, then:
\begin{align*} [(f \circ g)(x)]’ = f'[g(x)] \, g'(x) \qquad (x \in I) \end{align*}
(refer to the guide on Chain Rule for more detail)
If the function $f^{-1}$ is well-defined on an interval $I$, and the expression $\displaystyle \frac{1}{ f'[ f^{-1} (x) ] }$ makes sense on $I$ (i.e., for all $x \in I$, $f$ is differentiable at $f^{-1} (x)$, with the derivative being non-zero), then:
\begin{align*} [f^{-1}(x)]’ = \frac{1}{f'[f^{-1}(x)]} \qquad (x \in I) \end{align*}
(refer to the guide on Inverse Function Theorem for more detail)
For the most part, these rules are more than enough to handle the vast majority of functions one would encounter. However, when we look at our repertoire of functions, we see that something else is missing, namely:
What about the functions constructed via exponentiation?
Here, prompted by an unusual sense of urgency, we proceed to toy around with the idea of derivative of a power, subsequently ending up developing a rule precisely for that purpose. The name? Exponent Rule of course! Now, we bet that you haven’t seen this one yet — at least not in a standard calculus textbook or Khan Academy anyway!
Table of Contents
Exponent Rule for Derivative — Theory
Given a base function $f$ and an exponent function $g$ — both defined on an interval $I$ — one can construct the power function $f^g$ (i.e., $f$ raised to $g$), which is defined as long as $f(x)>0$ on $I$ (why?). In which case, the properties of logarithm warrant that:
\begin{align*} f(x)^{g(x)} & = e^{\ln \left[ f(x)^{g(x)} \right] } = e^{g(x) \ln f(x)} \end{align*}
which suggests that $\displaystyle e^{g(x) \ln f(x)}$ and $\displaystyle f(x)^{g(x)}$ can be used interchangeably on $I$.
More importantly though, in the case where $f$ and $g$ are both differentiable on $I$, using a combination of Chain Rule and Product Rule, we get that:
\begin{align*} \left( f(x)^{g(x)} \right)’ & = \left( e^{g(x) \ln f(x)} \right)’ \\ & = e^{g(x) \ln f(x)} \, [g(x) \ln f(x)]’ \\ & = f(x)^{g(x)} \left[ g'(x) \ln f(x) + f'(x) \frac{ g(x)}{f(x)} \right] \end{align*}
Too much $f$ and $g$? No worry. All we have shown is that the derivative of $f^g$ can be expressed in terms of the derivatives of $f$ and $g$ — and hence the Exponent Rule for derivatives!
Theorem — The Exponent Rule for Derivative
Given a base function $f$ and an exponent function $g$, if:
- The power function $f^g$ is well-defined on an interval $I$ (i.e.,$f$ and $g$ both well-defined on $I$, with $f>0$ on $I$)
- Both $f$ and $g$ are differentiable on $I$
then the function $f^g$ is differentiable on $I$ as well. In addition:
\begin{align*} (f^g)’ = f^g \left( g’ \ln f + f’ \frac{g}{f} \right) \qquad (x \in I) \end{align*}
In English, the Exponent Rule can be interpreted as follows:
The derivative of a power, is equal to the power itself times the following: the derivative of the exponent times the logarithm of the base, plus the derivative of the base times the exponent-base ratio.
And if that still sounds a bit pedantic, just know that the Exponent Rule basically guarantees that the derivative of $f^g$ — if exists — takes the form of $f^g (A+B)$, where:
- $A$ is obtained by taking the derivative of the exponent, times the logarithm of the base.
- $B$ is obtained by taking the derivative of the base instead, times the ratio with the exponent on the top.
In fact, with just a bit of practice, it’s possible to master the Exponent Rule as much as we do with the Quotient Rule — and this is not to mention the whole new world it opens up to our mental calculus fanatics!
Exponent Rule for Derivative — Applications
Traditionally, to evaluate the derivative of a power function, one would have to either resort to logarithmic differentiation, or base-e standardisation before differentiating it. With the advent of the Exponent Rule, both of these approaches basically become obsolete — not because they are irrelevant per se, but because they have already been carried out during the derivation of the Exponent Rule.
In what follows, we lay out 7 examples illustrating how the Exponent Rule can be used to streamline the differentiation process for power functions, thereby freeing up some of our brainpower and resources to other potentially-more-challenging tasks that are yet to come.
Example 1 — $\pi^x$
With the base function being $\pi$ and the exponent function $x$, the exponential function $\pi^x$ — which is defined on the entire real line — easily satisfies the preconditions laid out by the Exponent Rule. In which case, differentiating it using the Rule yields that:
\begin{align*} (\pi^x)’ & = \pi^x \left[ (x)’ \ln \pi + (\pi)’ \frac{x}{\pi} \right] = \pi^x \ln \pi \qquad (x \in \mathbb{R})\end{align*}
which shows that $\pi^x$ differentiates to itself along with some adjustment factor — a typical behavior among the exponential functions.
Now, is that a heavy-handed differentiation approach to a particularly-simple function? Actually, not really, for as it turns out, the alternative approaches would have been essentially the same — save perhaps a few more extra “patching” steps.
Finally, to celebrate our first successful execution of the Exponent Rule, we’ve cooked up the graphs of $\pi^x$ and its derivative here:
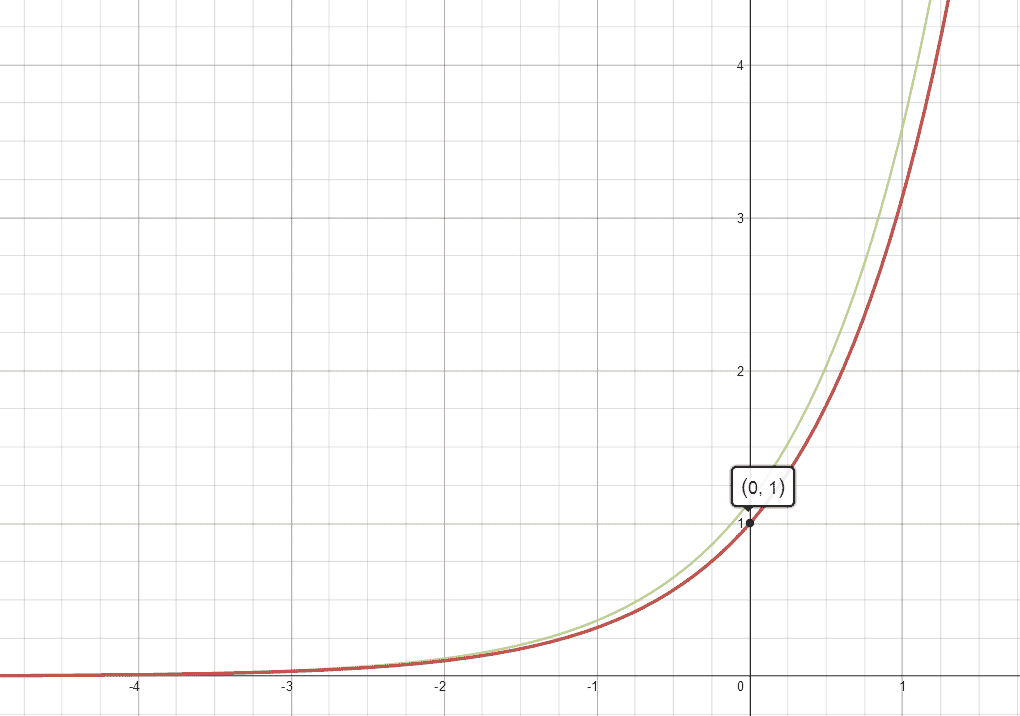
Example 2 — Exponential Function (Arbitrary Base)
Generalizing from the last example, we see that given the base function $b$ ($b>0, b \ne 1$) and the exponent function $x$, the exponential function $b^x$ — which is defined on the entire real line — can also be differentiated using the Exponent Rule as follows:
\begin{align*} (b^x)’ & = b^x \left[ (x)’ \ln b + (b)’ \frac{x}{b} \right] = b^x \ln b \qquad (x \in \mathbb{R})\end{align*}
which shows that in general, an exponential function differentiates to itself, along with the natural logarithm of its base.
Example 3 — $x^{\ln x}$
With the base function $x$ and the exponent function $\ln x$, the power function $\displaystyle x^{\ln x}$ unfortunately can be only defined on the set $\mathbb{R_+}$. However, this is really more of a blessing than a curse, as $\mathbb{R_+}$ happens to be the biggest domain under which both the base and the exponent function are differentiable anyway. In which case, applying the Exponent Rule yields that:
\begin{align*} (x^{\ln x})’ & = x^{\ln x} \left[ (\ln x)’ (\ln x) + (x)’\frac{\ln x}{x} \right] \\ & = x^{\ln x} \left[ \frac{\ln x}{x} + \frac{\ln x}{x} \right] \\ & = x^{\ln x} \, \frac{2 \ln x}{x} \qquad (x>0) \end{align*}
which is not too bad as a result. To be sure, here’s the graph of $\displaystyle x^{\ln x}$ and its derivative alongside with it:
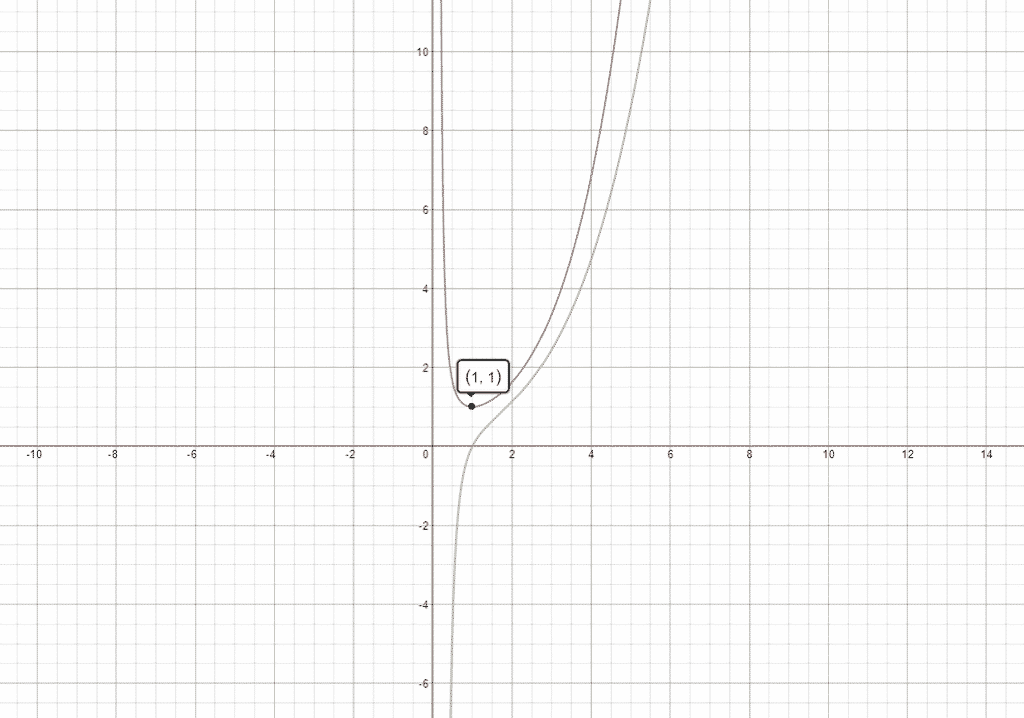
Example 4 — $(x^2+1)^{\sin x}$
There we go. Time to unleash the extravaganza! With the base function $x^2+1$ and the exponent function $\sin x$, the power function $\displaystyle (x^2+1)^{\sin x}$ — which is defined everywhere on $\mathbb{R}$ — has the added bonus that both the base and the exponent functions are differentiable on $\mathbb{R}$ as well. In which case, a single application of the Exponent Rule yields:
\begin{align*} \left( (x^2+1)^{\sin x}\right)’ & = (x^2+1)^{\sin x} \left[ (\sin x)’ \ln (x^2+1) + (x^2+1)’ \frac{\sin x}{x^2+1} \right] \\ & = (x^2+1)^{\sin x} \left[ \cos x \ln (x^2+1) + \frac{2x \sin x}{x^2+1} \right] \end{align*}
Interesting! Let’s plug them into our graphing application and see what kind of madness it produces in return!
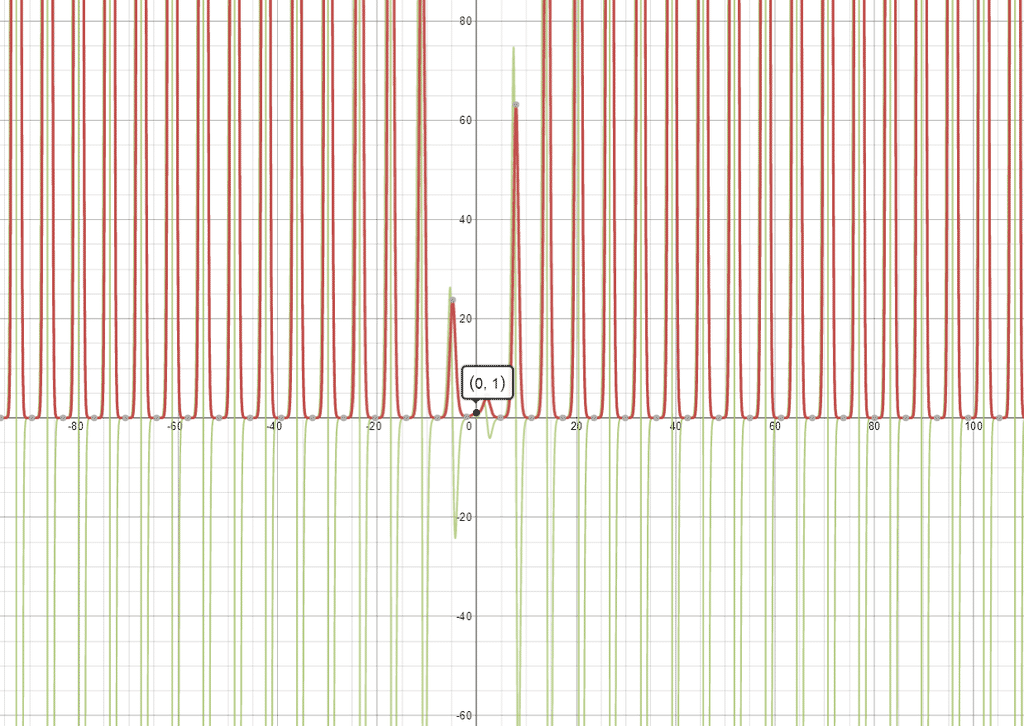
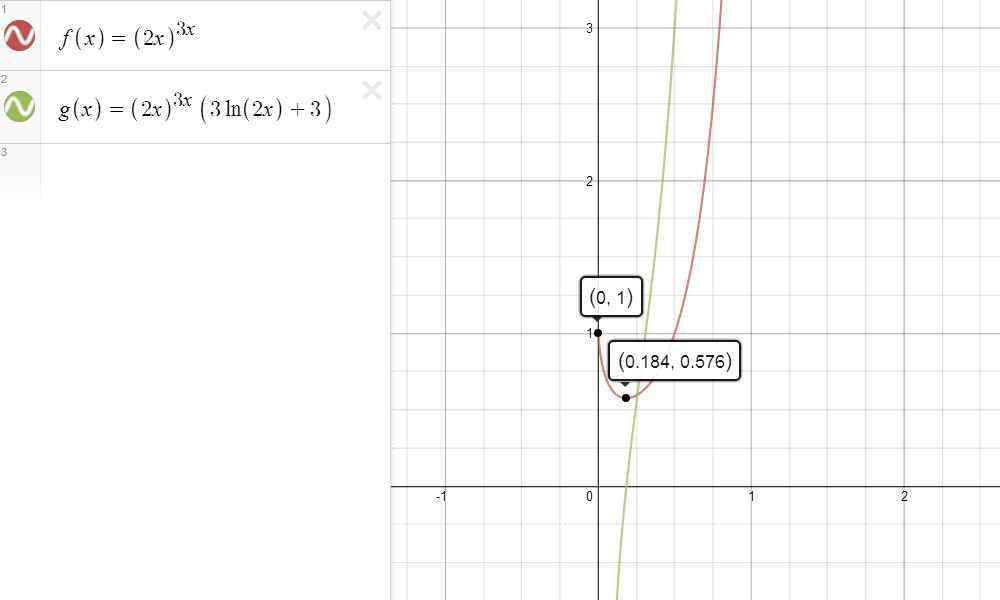
Example 5 — $(2x)^{3x}$
Running through our checklist as usual, we see that the base function $2x$ can only be positive on $\mathbb{R_+}$ (i.e., the set of positive real numbers). However, in doing so, we also found that both the base function $2x$ and the exponent function $3x$ are well-defined and differentiable on $\mathbb{R_+}$. As a result, the power function $\displaystyle (2x)^{3x}$ is differentiable on $\mathbb{R_+}$ as well, with its derivative obtainable through the use of Exponent Rule:
\begin{align*} \left[ (2x)^{3x}\right]’ & = (2x)^{3x} \left[ (3x)’ \ln (2x) + (2x)’ \frac{3x}{2x} \right] \\ & = (2x)^{3x} \left[ 3 \ln(2x) + 3 \right] \qquad (x>0) \end{align*}
Alternatively, we can also push the $3$ in the exponent function into the base function, as follows:
\begin{align*} (2x)^{3x} & = \left[{(2x)^3}\right]^x = (8x^3)^x \qquad (x>0)\end{align*}
in which case, the previous observations about the domain and differentiability still hold, and applying the Exponent Rule once again yields:
\begin{align*} \left[ (8x^3)^x \right]’ & = (8x^3)^x \left[ \ln (8x^3) + 24x^2 \frac{x}{8x^3} \right] \\ & = (2x)^{3x} \left[ \ln (8x^3) + 3 \right] \qquad (x>0) \end{align*}
which coincides with the derivative obtained a bit earlier. Magic!
Example 6 — ${\left( \sqrt{x}^{\cos x}\right)}^{\ln x}$
So, what about the cases involving higher exponentiation like this one? Well, no sweat here, as this is not a real nested power function anyway. Indeed, using the Generalized Power Rule for Logarithm, one can collapse it back into an ordinary power function as follows:
\begin{align*} {\left( \sqrt{x}^{\cos x}\right)}^{\ln x} & = \sqrt{x}^{\cos x \ln x} \qquad (x>0) \end{align*}
Once here, it can be seen that not only is $\displaystyle \sqrt{x}^{\, \cos x \ln x}$ well-defined on $\mathbb{R_+}$, but both the base function $\sqrt{x}$ and the exponent function $\cos x \ln x$ are differentiable on $\mathbb{R_+}$ as well. In which case, applying the Exponent Rule yields that:
\begin{align*} \left( \sqrt{x}^{\, \cos x \ln x} \right)’ & = \sqrt{x}^{\, \cos x \ln x} \Bigg[ \left( -\sin x \ln x + \frac{\cos x}{x} \right) \ln \sqrt{x} \\ & \phantom{ = } \;\; + \frac{1}{2\sqrt{x}} \frac{\, \cos x \ln x}{\sqrt{x}} \Bigg] \\ & = \sqrt{x}^{\, \cos x \ln x} \left[ -\frac{1}{2}\sin x (\ln x)^2 + \frac{\cos x \ln x}{x} \right] \qquad (x>0) \end{align*}
which gets a bit lengthy. But the point is that it is doable, so that if we put everything together, we get that:
\begin{align*} \left[ {\left( \sqrt{x}^{\, \cos x}\right)}^{\ln x} \right]’ & = \left( \sqrt{x}^{\, \cos x \ln x} \right)’ \\ & = {\left( \sqrt{x}^{\, \cos x}\right)}^{\ln x} \left[ -\frac{1}{2}\sin x (\ln x)^2 + \frac{\cos x \ln x}{x} \right] \qquad (x>0) \end{align*}
and here’s a picture of the graph as a bonus.
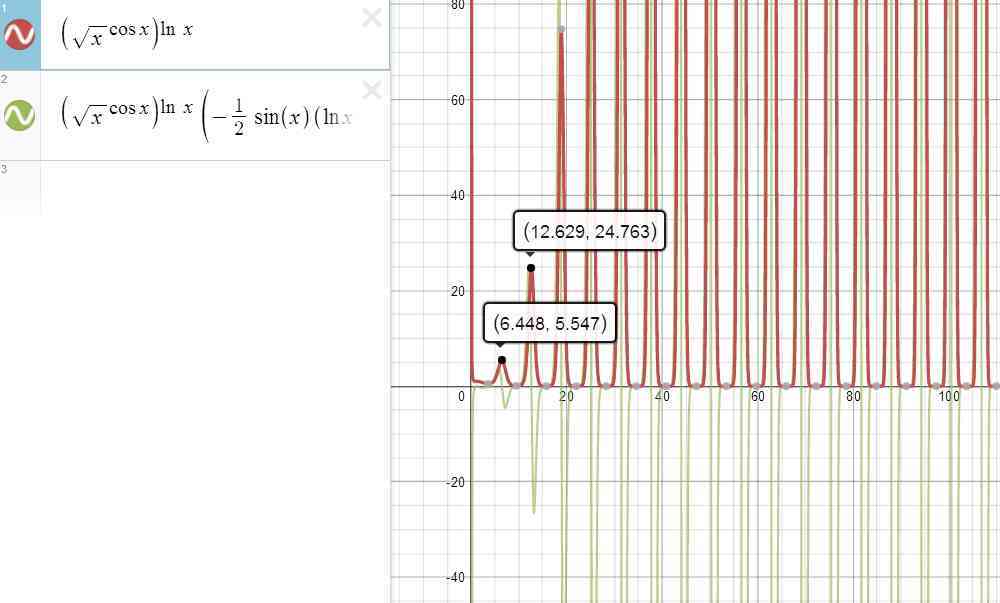
Example 7 — $\sqrt{x}^{\cos x^{\ln x}}$
Now you might be asking, “isn’t that the one we’ve just worked on a bit earlier?” Actually, not quite. This is due to the not-so-secret convention that: \[ \sqrt{x}^{\, \cos x^{\, \ln x}} \stackrel{df}{=} \sqrt{x}^{\, (\cos x^{\, \ln x} ) } \]
In this case, the Power Rule for logarithm simply won’t work. But then, that’s not to say that it precludes us from calculating the derivative recursively either.
To see how, let’s begin by focusing on the exponent function $\displaystyle \cos x^{\, \ln x}$, from which we can see that:
- $\ln x$ is only defined when $x>0$.
- $\cos x>0$ only when $\displaystyle -\frac{\pi}{2} < x < \frac{\pi}{2} \pmod{2\pi}$.
So that if we let $I$ denote the set satisfying both restrictions. That is,
\begin{align*}I \stackrel{df}{=} \left\{ x \in \mathbb{R_+} \mathrel{\Big|} -\frac{\pi}{2} < x < \frac{\pi}{2} \,\, (\mathrm{mod \ } 2\pi ) \right\} \end{align*}
then one can see that $\displaystyle \cos x^{\, \ln x}$ is well-defined on $I$, with both $\cos x$ and $\ln x$ being differentiable on $I$ as well. In which csae, the Exponent Rule kicks in, yielding that:
\begin{align*} \left( \cos x^{\, \ln x} \right)’ & = \cos x^{\, \ln x} \left[ \frac{1}{x} \ln (\cos x) + (-\sin x) \frac{\ln x}{\cos x} \right] \\ & = \cos x^{\, \ln x} \left[ \frac{\ln (\cos x)}{x} – \tan x \ln x \right] \qquad (x \in I) \end{align*}
which takes care of the derivative of the exponent function. Now, if we just backtrack a bit to the original function, then it shouldn’t be hard to to see that:
- $\displaystyle \sqrt{x}^{\, (\cos x^{\, \ln x})}$ is well-defined on $I$.
- Both the base function $\sqrt{x}$ and the exponent function $\cos x^{\, \ln x}$ are differentiable on $I$.
which can only mean one thing — that $\displaystyle \sqrt{x}^{\, (\cos x^{\ln x})}$ is very well differentiable on $I$ as well. Here, applying the Exponent Rule a second time, we obtain that:
\begin{align*} \left[ \sqrt{x}^{\, ({\cos x}^{\, \ln x} )} \right]’ & = \sqrt{x}^{\, ({\cos x}^{\, \ln x} )} \left[ \left( {\cos x}^{\, \ln x}\right)’ \ln \sqrt{x} + \frac{1}{2\sqrt{x}} \frac{{\cos x}^{\, \ln x}}{\sqrt{x}} \right] \\ & = \cdots \end{align*}
Well, guess we’ll stop here and leave the algebra up to you. But hey, if you are proficient enough to have gone this far, you can finish that up right? 🙂
And for your curiosity, here’s the graph of the original function and its derivative for the record. Notice the stark contrast between this and the graphs from Example 6.
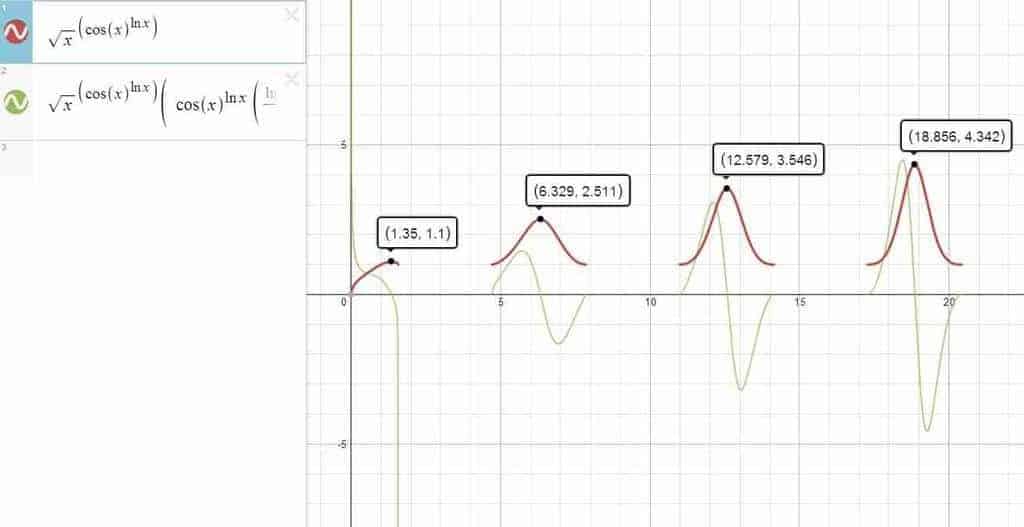
Closing Words
Yes. That was a bit of symbol-crunching, but hopefully it illustrates why the Exponent Rule can be a valuable asset in our arsenal of derivative rules. While for simple power function, this approach might seem like an overkill, for repeatedly-exponentiated power functions with one nested inside another, it becomes readily apparent that the Exponent Rule is absolutely the way to go.
In addition to automating the differentiation process for power functions, the Exponent Rule — especially when combined with other traditional derivative rules — can really do wonder in terms of tapping into functions that are previously too intimidating / tedious to tackle — such as the ones we have a hard time finding in a typical calculus textbook for instance. 🙂
In any case, let’s leave it at that and call it a day for now. For the sake of completeness, here’s an interactive table summarizing what we have discovered thus far:
| Constant Rule |
| Power Rule |
| Sum Rule |
| Difference Rule |
| Product Rule |
| Reciprocal Rule |
| Quotient Rule |
| Chain Rule |
| Inverse-Function Rule |
Given a base function $f$ and an exponent function $g$, if:
- The power function $f^g$ is well-defined on an interval $I$ (i.e.,$f$ and $g$ both well-defined on $I$, with $f>0$ on $I$)
- Both $f$ and $g$ are differentiable on $I$.
then the function $f^g$ is differentiable on $I$ as well. In addition:
\begin{align*} (f^g)’ = f^g \left( g’ \ln f + f’ \frac{g}{f} \right) \qquad (x \in I) \end{align*}
| $\displaystyle (\pi^x)’ = \pi^x \ln \pi \quad (x \in \mathbb{R})$ |
| $\displaystyle (b^x)’ = b^x \ln b \quad (x \in \mathbb{R})$ |
| $\displaystyle (x^{\ln x})’ = x^{\ln x} \, \frac{2 \ln x}{x} \quad (x>0) $ |
| $\displaystyle \left[ (x^2+1)^{\sin x} \right]’ = (x^2+1)^{\sin x} \left[ \cos x \ln (x^2+1) + \frac{2x \sin x}{x^2+1} \right] \quad (x \in \mathbb{R}) $ |
| $\displaystyle \left[ (2x)^{3x}\right]’ = (2x)^{3x} \left[ 3 \ln(2x) + 3 \right] \quad (x>0) $ |
| $\displaystyle \left[ {\left( \sqrt{x}^{\, \cos x}\right)}^{\ln x} \right]’ = {\left( \sqrt{x}^{\, \cos x}\right)}^{\ln x} \left[ -\frac{1}{2}\sin x (\ln x)^2 + \frac{\cos x \ln x}{x} \right] \quad (x>0) $ |
| $\displaystyle \left[ \sqrt{x}^{\, ({\cos x}^{\, \ln x} )} \right]’ = $ you know |
In brief, while relatively unknown, the Exponent Rule can be a powerful differentiation tool at our disposal. Not only does it avoid the circularity of logarithmic differentiation, but it also allows us to differentiate faster when a large chunk of generalized powers are involved.
Sure, the rule might look a little bit intimidating at first, but once it’s mastered, it’s almost impossible to imagine differentiating without it. After all, every differentiation rule is there to save us from repeating the same procedures over and over, and the Exponent Rule is not much less elegant from any other!

I couldn’t agree more with your closing statement — at first I felt why should anyone have to remember another rule when they could just perform logarithmic differentiation, but having solved those examples, I can see this technique is much faster than logarithmic differentiation! I suppose one must succumb to making rules if they make life easy 🙂
A few things I feel I should point out are:
You misspelled derivative as derivcative in example 3 (above the graph)
The links on the table or the rules section at the top just link back to the top of the article.
As always, I enjoyed this derivative module!
Thank you 🙂
This is getting better. Thanks! Interesting, the table works in the backend for some reason. We’ll look that up.
any update on this?
Yep. Now we’ve 7 examples of the Exponent Rule for your pleasure!