In mathematics, calculus formalizes the study of continuous change, while analysis provides it with a rigorous foundation in logic. The following list documents some of the most notable symbols and notations in calculus and analysis, along with each symbol’s usage and meaning.
For readability purpose, these symbols are categorized by topic and function into tables. Other comprehensive lists of math symbols — as categorized by subject and type — can be also found in the relevant pages below (or in the navigational panel).
Table of Contents

Prefer the PDF version instead?
Get the master summary of mathematical symbols in eBook form — along with each symbol’s usage and LaTeX code.
Constants and Variables
In calculus and analysis, constants and variables are often reserved for key mathematical numbers and arbitrarily small quantities. The following table documents some of the most notable symbols in these categories — along with each symbol’s example and meaning.
| Symbol Name | Explanation | Example |
|---|---|---|
| $e$ | Euler’s number e | $\displaystyle e = \frac{1}{0!} + \frac{1}{1!} + \cdots$ |
| $\pi$ (Pi) | Archimedes’ constant | $\dfrac{\pi^2}{6} = \dfrac{1}{1^2} + \dfrac{1}{2^2} +$ $\dfrac{1}{3^2} + \dfrac{1}{4^2} + \cdots$ |
| $i$ | Imaginary unit | By Euler’s formula, $e^{\pi i} = \cos \pi + i \sin \pi$. |
| $\gamma$ (Gamma) | Euler–Mascheroni constant | $\displaystyle \left( \sum_{k=1}^{n} \dfrac{1}{k}-\ln n \right) \to$ $\gamma \approx 0.577$ |
| $\Omega$ (Capital omega) | Omega constant | $\Omega e^{\Omega} = 1$ |
| $m$ | Variable for slope | $m = \dfrac{y_2-y_1}{x_2-x_1}$ |
| $h$, $\Delta x$, $\delta x$ | Limiting variables for difference quotient | $\displaystyle \lim_{h \to 0} \dfrac{f(x+h)-f(x)}{h}$ |
| $L$ | Variable for limit | If $f(x) \to L$, then $f(x)^2 \to L^2$. |
| $\varepsilon$ (Epsilon), $\delta$ (Delta) | Variables for arbitrarily small quantities | $\forall \varepsilon \, \exists \delta \, \big( 0<|x-x_0|<\delta$ $\implies |f(x)-L|< \varepsilon \big) $ |
| $a, b$ | Variables for endpoints in intervals and definite integrals | $\displaystyle \int_a^b 2x \, \mathrm{d}x= b^2-a^2$ |
| $C$ | Constant of integration | $\displaystyle \int \dfrac{1}{x} \, \mathrm{d} x = \ln |x| + C$ |
Sequence, Series and Limit
The concepts of sequence, series and limit form the foundation of calculus (and by extension real and complex analysis). The following table features some of the most common symbols related to these topics — along with each symbol’s usage and meaning.
| Symbol Name | Explanation | Example |
|---|---|---|
| $+\infty$ | Positive infinity | $\dfrac{1}{1} + \dfrac{1}{2} + \cdots = \infty$ |
| $-\infty$ | Negative infinity | As $x \to -\infty$, $e^x \to 0$. |
| $(a_n), (b_n), (c_n)$ | Sequences | $\displaystyle (a_n)_{n=0}^\infty =$ $(a_0, a_1, a_2, \ldots)$ |
| $\displaystyle \sum_{n = i}^k a_n$ | Series | $\displaystyle \sum_{n=1}^k b_n = \\ b_1 + \cdots + b_k$ |
| $\| \mathrm{x}-\mathrm{y}\|$ | Euclidean distance between points $\mathrm{x}$ and $\mathrm{y}$ | $\| \mathrm{x}-\mathrm{x}_0 \| < 1 \implies$ $| f(\mathrm{x})-f(\mathrm{x}_0) | < 2 $ |
| $d(x, y)$ | Distance function | $d(x, y) = |x-y|$ |
| $\displaystyle \lim_{n \to \infty} a_n$ | Limit of sequence | $\displaystyle \lim_{n \to \infty} \left(1+\dfrac{1}{n}\right)^n = e$ |
| $\displaystyle \lim_{k \to \infty} \sum_{n=i}^k a_n, \sum_{n=i}^{\infty} a_n$ | Limit of series | $\displaystyle \sum_{n=0}^{\infty} \dfrac{1}{2^n} = 2$ |
| $\mathrm{x} \to a$ | Variable $\mathrm{x}$ tends to $a$ | $\lim (a_n) = 1/4$ as $n \to \infty$. |
| $f(x) \to L$ | Function $f(x)$ tends to limit $L$ | Since $g(x)$ is continuous at $c$, $g(x) \to g(c)$ as $x \to c$. |
| $\displaystyle \lim_{x \to a} f(x)$ | Limit of function $f(x)$ as $x$ tends to $a$ | $\displaystyle \lim_{x \to 0} \dfrac{\sin x}{x} = 1$ |
| $\displaystyle \lim_{x \to a^+} f(x)$, $\displaystyle \lim_{x \, \downarrow \, a} f(x)$ | Right-sided limit (Limit of $f(x)$ as $x$ tends to $a$ from the right) | $\displaystyle \lim_{x \to 3^+} \dfrac{1}{x-3} = +\infty$ |
| $\displaystyle \lim_{x \to a^-} f(x)$, $\displaystyle \lim_{x \, \uparrow \, a} f(x)$ | Left-sided limit (Limit of $f(x)$ as $x$ tends to $a$ from the left) | $\displaystyle \lim_{x \to 0^-} \sqrt{-x} = 0$ |
| $\min (A)$ | Minimum of set $A$ | $\min (a_n) + \min (b_n) \le$ $\min (a_n + b_n)$ |
| $\max (A)$ | Maximum of set $A$ | If $f$ is continuous on $[a, b]$, then $\max (f(x))$ exists on that interval. |
| $\inf (A)$ | Greatest lower bound of set $A$ | $\inf\left(\left\{\dfrac{1}{n} \, \middle| \, n \in \mathbb{N} \right\}\right)$ $= 0$ |
| $\sup (A)$ | Least upper bound of set $A$ | $\sup \left(\left\{x \in \mathbb{Q} \, \middle| \, x^2 < 2 \right\}\right)$ $= \sqrt{2}$ |
| $\liminf a_n$ | Limit inferior of sequence $a_n$ | $\displaystyle \liminf_{n \to \infty} \dfrac{2}{n+1} =$ $\displaystyle \lim_{n \to \infty} 0$ |
| $\limsup a_n$ | Limit superior of sequence $a_n$ | $\displaystyle \limsup_{n \to \infty} b_n =$ $\displaystyle \lim_{n \to \infty} \left( \sup_{m \ge n} b_m \right)$ |
Derivative and Integral
The field of calculus (e.g., multivariate/vector calculus, differential equations) is often said to revolve around two opposing but complementary concepts: derivative and integral. The following tables document the most notable symbols related to these — along with each symbol’s usage and meaning.
(For a review on function and related operators, see function-related operators.)
Univariate Derivative-related Symbols
| Symbol Name | Explanation | Example |
|---|---|---|
| $f^{\prime}(\mathrm{x}), f^{\prime \prime}(\mathrm{x}), f^{(n)}(\mathrm{x})$ | First, second and $n$th derivative of $f$ at $\mathrm{x}$ (Lagrange’s notation) | $f'(c) =$ $\displaystyle \lim_{h \to 0} \dfrac{f(c + h)-f(c)}{h}$ |
| $\dfrac{d}{d\mathrm{x}} f, \dfrac{df}{d\mathrm{x}}$ | Derivative of function $f$ in terms of $\mathrm{x}$ (Leibniz’s notation) | $\dfrac{d}{dx} f = f'(x)$ |
| $\dfrac{d^n}{d\mathrm{x}^n} f, \dfrac{d^n f}{d\mathrm{x}^n}$ | Nth derivative of function $f$ in terms of $\mathrm{x}$ (Leibniz’s notation) | $\dfrac{d^2 f}{dx^2} = \dfrac{d}{dx}\left(\dfrac{df}{dx}\right)$ |
| $\dot{y}$, $\ddot{y}$, $\overset{n}{\dot{y}}$ | First, second and $n$th derivative of $y$ in terms of time variable $t$ (Newton’s notation) | $\ddot{y}= \dfrac{d^2 y}{dt^2}$ |
| $D(f), D^2(f), D^{n}(f)$ | First, second and $n$th derivative of $f$ (Euler’s notation) | $D^2(f) = D(D(f))$ |
| $\Delta \mathrm{x}$ | Increment in variable $\mathrm{x}$ | $\Delta y \approx f'(x) \Delta x$ |
| $d \mathrm{x}$ | Differential of variable $\mathrm{x}$ | $dy = \dfrac{dy}{dx}\, dx$ |
Multivariate Derivative-related Symbols
| Symbol Name | Explanation | Example |
|---|---|---|
| $f_\mathbf{x}$ | Partial derivative of $f$ in terms of $\mathbf{x}$ (Lagrange’s notation) | $\displaystyle f_x (a, b) = \lim_{h \to 0}$ $\frac{f(a+h, \, b) \, – \, f(a,\, b)}{h}$ |
| $\dfrac{\partial}{\partial \mathrm{x}} f, \dfrac{\partial f}{\partial \mathrm{x}}$ | Partial derivative of $f$ in terms of $\mathrm{x}$ (Leibniz’s style) | If $f$ has continuous second partial derivatives, then $\dfrac{\partial}{\partial y}\dfrac{\partial f}{\partial x} = \dfrac{\partial}{\partial x}\dfrac{\partial f}{\partial y}$ |
| $\dfrac{\partial^n}{\partial \mathrm{x}^ n} f, \dfrac{\partial^n f}{\partial \mathrm{x}^n}$ | Nth partial derivative of $f$ in terms of $\mathrm{x}$ (Leibniz’s style) | $\dfrac{\partial^2 f}{\partial y^2} = \dfrac{\partial}{\partial y}\dfrac{\partial f}{\partial y}$ |
| $\partial_x f$ | Partial derivative of $f$ in terms of $x$ (Euler’s notation) | $\partial_{xy} f = \dfrac{\partial}{\partial y} \dfrac{\partial f}{\partial x}$ |
| $\nabla_{\mathbf{v}} f$ | Directional derivative of $f$ with respect to direction $\mathbf{v}$ | $\nabla_{\mathbb{v}} f(\mathbf{x}) =$ $\displaystyle \lim_{h \to 0} \dfrac{f(\mathbf{x}+h\mathbf{v})-f(\mathrm{x})}{h}$ |
| $\partial \mathrm{x}$ | Partial differential of variable $\mathrm{x}$ | $\dfrac{\partial f}{\partial x} dx \le df$ |
| $df$ | Total differential of function $f$ | $df = \dfrac{\partial f}{\partial x_1} dx_1 +$ $\displaystyle \cdots + \dfrac{\partial f}{\partial x_n} dx_n$ |
| $\nabla f, \mathrm{grad}\,f$ | Gradient of function $f$ | $\nabla f =$ $\left( \dfrac{\partial f}{\partial x_1}, \ldots, \dfrac{\partial f}{\partial x_n} \right)$ |
| $\Delta f$ | Laplace operator of function $f$ | $\displaystyle \Delta f = \sum_{i=1}^n \dfrac{\partial^2 f}{\partial x_i^2}$ |
| $\nabla \cdot \mathbf{F}, \mathrm{div}\, \mathbf{F}$ | Divergence of vector field $\mathbf{F}$ | $\nabla \cdot \mathbf{F} = \dfrac{\partial F_x}{\partial x} +$ $\dfrac{\partial F_y}{\partial y} + \dfrac{\partial F_z}{\partial z}$ |
| $\nabla \times \mathbf{F}, \mathrm{curl} \, \mathbf{F}$ | Curl of vector field $\mathbf{F}$ | $\nabla \times \mathbf{F} =$ $\left( \dfrac{\partial}{\partial x}, \dfrac{\partial}{\partial y}, \dfrac{\partial}{\partial z} \right) \times$ $\left( F_x, F_y, F_z \right)$ |
Derivative/Integral-related Shorthands
| Symbol Name | Explanation | Example |
|---|---|---|
| $\displaystyle \left. f(x) \right|_{x = a}$ | Shorthand for ‘$f(x)$ with $x$ substituted by $a$’ | $\displaystyle \left. f'(x) \right|_{x =g(t)} =$ $f'(g(t))$ |
| $\displaystyle \left[f(x)\right]_{a}^{b}$ | Shorthand for ‘$f(b)-f(a)$’ | $\left[\dfrac{x^2}{2}\right]_{1}^{\pi} = \dfrac{\pi^2}{2}-\dfrac{1}{2}$ |
Univariate Integral-related Symbols
| Symbol Name | Explanation | Example |
|---|---|---|
| $\displaystyle \int_a^b f(x) \, dx$ | Integral of function $f$ with respect to $x$ from $a$ to $b$ | $\displaystyle \int_0^{\infty} \dfrac{1}{1+x^2} \, dx = \dfrac{\pi}{2}$ |
| $\displaystyle \int f(x) \, dx$ | Indefinite integral of function $f$ with respect to $x$ | $\displaystyle \int \cos y \, dy = \\ \sin y + C$ |
| $F(x)$ | Antiderivative of function $f$ | For all constants $c$, $(F(x) + c)’ = f(x)$. |
| $(Jf)(x)$ | Integration operator (Integral function of $f$) | $(Jf)(x) =$ $\displaystyle \int_0^x f(t) \, dt$ |
Multivariate Integral-related Symbols
| Symbol Name | Explanation | Example |
|---|---|---|
| $\displaystyle \int_C f(\mathbf{r}) \, ds$ | Line integral of function $f$ along curve $C$ (under parametrization $\mathbf{r}$) | $\displaystyle \int_C f(\mathbf{r}) \, d s =$ $\displaystyle \int_a^b f(\mathbf{r}(t)) \, |\mathbf{r}'(t)| \, d t$ |
| $\displaystyle \int_{C} f(z) \, dz$, $\displaystyle \oint_{C} f(z) \, dz$ | Contour integral of function $f$ along curve $C$ | $\displaystyle \int_{\gamma} f(z) \, dz =$ $\displaystyle \int_a^b f(\gamma(t)) \, \gamma'(t) \, dt$ |
| $\displaystyle \int_C \mathbf{F}(\mathbf{r}) \cdot d\mathbf{r}$ | Line integral of vector field $\mathbf{F}$ along curve $C$ | $\displaystyle \int_C \mathbf{F}(\mathbf{r}) \cdot d \mathbf{r} =$ $\displaystyle \int_a^b \mathbf{F}(\mathbf{r}(t)) \cdot \mathbf{r}'(t) \, d t$ |
| $\displaystyle \iint_D f \, dA$ | Area integral of function $f$ over domain $D$ | $\displaystyle \iint_{[0, 1] \times [0, 1]} f(x, y) \, dA$ $= \displaystyle \!\!\! \int_0^1\!\!\! \int_0^1 \!\!\! f(x,y) \, dx \, dy$ |
| $\displaystyle \iint_D f(\mathbf{r}) \, dS$ | Surface integral of function $f$ over domain $D$ (under parametrization $\mathbf{r}$) | $\displaystyle \iint_D f(\mathbf{r}) \, dS =$ $\displaystyle \!\!\! \int_a^b \!\!\! \int_c^d \!\!\! f(\mathbf{r}(s, t))$ $\left\| \dfrac{\partial \mathbf{r}}{\partial s} \times \dfrac{\partial \mathbf{r}}{\partial t} \right\| ds \, dt $ |
| $\displaystyle \iiint_D f \, dV$ | Volume integral of function $f$ over domain $D$ | $\displaystyle \iiint_{x^2+y^2+z^2 \le R^2} 1 \, dV$ $= \dfrac{4}{3}\pi R^3$ |
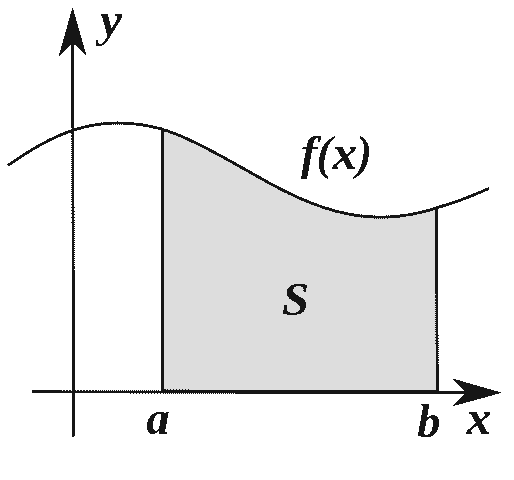
Standard integral 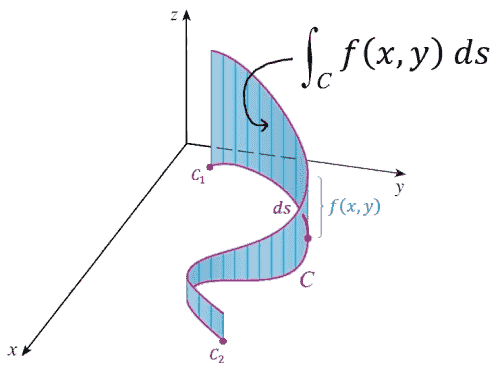
Line integral 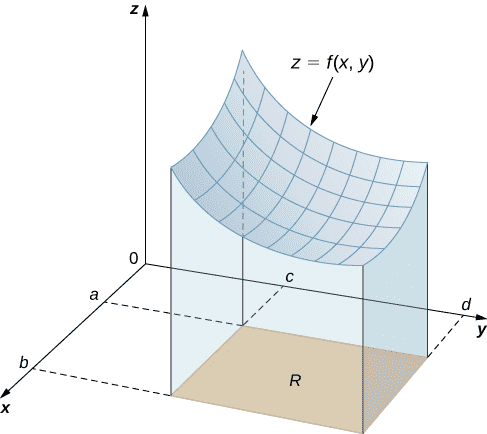
Area integral 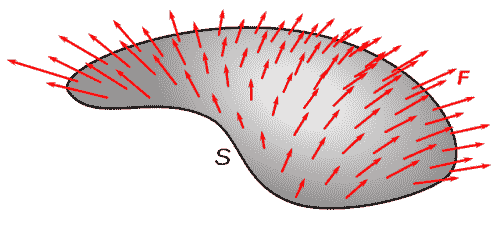
Surface integral
(of vector field)
Asymptotic Analysis
In calculus and analysis, the need for comparing the rates of growth of different functions leads to the study of asymptotic analysis. The following table documents some of the most notable symbols related to this topic — along with each symbol’s usage and meaning.
| Symbol Name | Explanation | Example |
|---|---|---|
| $f \equiv g$ | Function $f$ is identically equal to function $g$ | $f \equiv g \iff$ $\mathrm{dom}(f)=\mathrm{dom}(g)$ $\mathrm{and}\, f(x)=g(x) $ $\left( \forall x \in \mathrm{dom}(f) \right)$ |
| $f \sim g$ | Function $f$ is asymptotically equal to function $g$ | $f \sim g \iff $ $\displaystyle \lim_{x \to \infty} \dfrac{f(x)}{g(x)} = 1$ |
| $f \ll g, f \in O(g)$ | $f$ is asymptotically bounded above by $g$ ($f$ is in the big-O of $g$) | $f \ll g \iff \exists k > 0$ $|f(x)| \le k |g(x)|$ $(\forall x \ge x_0)$ |
| $f \gg g, f \in \Omega(g)$ | $f$ is asymptotically bounded below by $g$ ($f$ is in the big-Omega of $g$) | $f \gg g \iff \exists k > 0$ $|f(x)| \ge k |g(x)|$ $(\forall x \ge x_0)$ |
| $f \in \Theta(g)$ | $f$ is asymptotically bounded above and below by $g$ ($f$ is in the big-Theta of $g$) | $f \in \Theta(g) \iff$ $f \ll g \: \mathrm{and} \: f \gg g$ |
| $f \in o(g)$ | $f$ is asymptotically dominated by $g$ ($f$ is in the small-O of $g$) | $f \in o(g)$ if and only if for all $k > 0$, $|f(x)| < k \, |g(x)|$ (for all $x \ge x_0$). |
| $f \in \omega(g)$ | $f$ asymptotically dominates $g$ ($f$ is in the small-Omega of $g$) | $f \in \omega(g)$ if and only if for all $k > 0$, $|f(x)| > k \, |g(x)|$ (for all $x \ge x_0$). |
The following table features some of the most common functions arranged according to their asymptotic hierarchy — where each function is asymptotically dominated by what follows it:
| Function | Function |
|---|---|
| $1$ | $x\log x$ |
| $\log(\log x)$ | $x^2$ |
| $\log x$ | $x^k \; (k>2)$ |
| $(\log x)^k \; (k > 1)$ | $a^x \; (a>1)$ |
| $x^c \; (0<c<1)$ | $n!$ |
| $x$ | $x^x$ |
Key Functions and Transforms
In calculus and analysis, one often makes reference to a wide range of key functions and transforms. The following table documents the most notable of these — along with each symbol’s usage and meaning.
(For a review on elementary functions, see key functions in algebra.)
Key Functions
| Function Name | Explanation | Example |
|---|---|---|
| $\mathrm{sgn}(x)$ | Sign function | $\mathrm{sgn}(x) =$ $\begin{cases} -1 & x < 0 \\ 0 & x=0 \\ 1 & x>0 \end{cases}$ |
| $\mathrm{atan2}(y, x)$ | 2-argument arctangent function | $\mathrm{atan2}(1, 0) = \pi /2$ |
| $\mathrm{B}(x ,y)$ | Beta function | $\mathrm{B}(x, y) =$ $\displaystyle \!\!\! \int_0^1 t^{x-1}(1-t)^{y-1} \, dt$ |
| $\Gamma (x)$ | Gamma function | $\Gamma(z) =$ $\displaystyle \int_0^{\infty} x^{z-1}e^{-x}\, dx$ |
| $\mathrm{sinc}(x)$ | Sinc function | $\mathrm{sinc}(x) = \dfrac{\sin x}{x}$ |
| $\mathrm{Si}(x)$ | Sine integral | $\mathrm{Si}(x) = \displaystyle \int_0^x \dfrac{\sin t}{t} \, dt$ |
| $\mathrm{erf}(x)$ | Error function | $\mathrm{erf}(x) =$ $\displaystyle \dfrac{2}{\sqrt{\pi}} \int_{0}^x e^{-t^2} \, dt$ |
| $\zeta (s)$ | Riemann zeta function | $\zeta(s) = \displaystyle \sum_{n=1}^{\infty} \dfrac{1}{n^s}$ |
| $f \ast g$ | Convolution of functions $f$ and $g$ | $(f \ast g) (x) =$ $\displaystyle \!\!\! \int_{-\infty}^{\infty} f(t) g(x-t) \, dt$ |
| $\delta (x)$ | Dirac delta function | Loosely speaking, $\delta (x) = 0$ for all $x \ne 0$ and $\int_{-\infty}^{\infty} \! \delta(x) \, dx = 1$. |
| $H(x)$ | Heaviside step function | $H(x) = \displaystyle \int_{-\infty}^x \delta(s) \, ds$ |
Key Transforms
| Symbol Name | Explanation | Example |
|---|---|---|
| $\mathcal{L}\{f\}$ | Laplace transform of function $f$ | $\mathcal{L}\{f\}(s) =$ $\displaystyle \int_0^{\infty} f(t)e^{-st} \, dt$ |
| $\mathcal{L}^{-1}\{F\}$ | Inverse Laplace transform of function $F$ | If $\mathcal{L}\{f\} = F(s)$, then $\mathcal{L}^{-1}\{F\} = f(t)$. |
| $\mathcal{F}\{f\}$, $\hat{f}$ | Fourier transform of function $f$ | $\mathcal{F}\{f\}(t) =$ $\displaystyle \int_{-\infty}^{\infty} f(x)e^{-2\pi i t x} \, dx$ |
For the master list of symbols, see mathematical symbols. For lists of symbols categorized by type and subject, refer to the relevant pages below for more.
- Arithmetic and Common Math Symbols
- Geometry and Trigonometry Symbols
- Logic Symbols
- Set Theory Symbols
- Greek, Hebrew, Latin-based Symbols
- Algebra Symbols
- Probability and Statistics Symbols
- Calculus and Analysis Symbols

Prefer the PDF version instead?
Get the master summary of mathematical symbols in eBook form — along with each symbol’s usage and LaTeX code.
Additional Resources
- Definitive Guide to Learning Higher Mathematics: A standalone, 10-principle framework for tackling higher mathematical learning, thinking and problem solving efficiently
- 10 Commandments of Higher Mathematical Learning: An illustrated web guide on 10 scalable rules for learning higher mathematics
- Ultimate LaTeX Reference Guide: A definitive reference guide to make the LaTeXing process more efficient and less painful
- Definitive Glossary of Higher Math Jargon: Foundational higher math concepts in 106 terms


Really very useful
Glad it helped Jeya!
The sources are very useful
Hi jmatsu. Glad you like them!