Geometry and trigonometry are branches of mathematics concerned with geometrical figures and angles of triangles. The following list documents some of the most notable symbols in these topics, along with each symbol’s usage and meaning.
For readability purpose, these symbols are categorized by their function into tables. Other comprehensive lists of math symbols — as categorized by subject and type — can be also found in the relevant pages below (or in the navigational panel).
Table of Contents

Prefer the PDF version instead?
Get the master summary of mathematical symbols in eBook form — along with each symbol’s usage and LaTeX code.
Point/Line-related Symbols
In geometry, points and lines form the foundation of more complex geometrical figures such as triangles, circles, quadrilaterals and polygons. The following table documents some of the most notable symbols related to these — along with each symbol’s meaning and example.
| Symbol Name | Explanation | Example |
|---|---|---|
| $A$, $B$, $C$, $D$, $P$, $Q$, $R$, $S$ | Variables for points | If $P_1 =P_2$, then $\overline{P_1 Q} = \overline{P_2 Q}$. |
| $\ell$ | Variable for lines | $\ell_1 \parallel \ell_2$ |
| $\overleftrightarrow{AB}$ | (Infinite) line formed by points $A$ and $B$ | $\overleftrightarrow{AB}=\overleftrightarrow{BA}$ |
| $\overline{AB}$ | Line segment between points $A$ and $B$ | $\overline{AB} \cong \overline{PQ}$ |
| $\overrightarrow{AB}$ | Ray from point $A$ to point $B$ | $\overrightarrow{AB} \ne \overrightarrow{BA}$ |
| $|AB|$ | Distance from point $A$ to point $B$ | $|BC| \le \\ |AB| + |AC|$ |
| $\ell_1 \parallel \ell_2$ | Lines $\ell_1$ and $\ell_2$ are parallel | If $\square ABCD$ is a parallelogram, then $\overline{AB} \parallel \overline{CD}$. |
| $\ell_1 \nparallel \ell_2$ | Lines $\ell_1$ and $\ell_2$ are non-parallel | If $\overleftrightarrow{PQ} \nparallel \overleftrightarrow{RS}$, then they must intersect at a point $A$. |
| $\ell_1 \perp \ell_2$ | Lines $\ell_1$ and $\ell_2$ are perpendicular | If $\overline{AB} \perp \overline{BC}$, then $|AC|^2 = |AB|^2 + \\ |BC|^2.$ |
| $\ell_1 \not\perp \ell_2$ | Lines $\ell_1$ and $\ell_2$ are non-perpendicular | If $\overline{AB} \not\perp \overline{BC}$, then $\square ABCD$ is not a rectangle. |
Angle-related Symbols
An angle essentially corresponds to an “opening” of a geometrical figure, whose quantification leads to much development in geometry and trigonometry. The following table documents some of the most notable symbols related to angles — along with each symbol’s meaning and example.
| hSymbol Name | Explanation | Example |
|---|---|---|
| $a, b, c$, $\alpha$ (alpha), $\beta$ (beta), $\gamma$ (gamma), $\theta$ (theta), $\phi$ (phi) | Variables for angles | $\alpha + \beta < \gamma$ |
| $^{\circ}$ | Degree symbol | $\alpha = 180^{\circ} – \beta$ |
| $\mathrm{rad}$ | Radian symbol | $\pi \, \mathrm{rad} = 180^{\circ}$ |
| $\mathrm{grad}$, $^{\mathrm{g}}$ | Gradian symbol | $100 \, \mathrm{grad} = 90^{\circ}$ |
| $\angle ABC$ | Angle formed by points $A$, $B$ and $C$ | $\angle ABC = \angle CBA$ |
| $\angle P$ | Interior angle at point $P$ | $m \angle P + m \angle Q = 90^{\circ}$ |
| $\measuredangle ABC$, $m\angle ABC$ | Measure of angle formed by points $A$, $B$ and $C$ | $\measuredangle PQR \approx 54^{\circ}$ |
| $\sphericalangle ABC$ | Spherical angle formed by points $A$, $B$ and $C$ | If $P$, $Q$, $R$ lie on a sphere, then $\sphericalangle PQR$ is the spherical angle between $\overparen{PQ}$ and $\overparen{QR}$. |
| $’$ | Arcminute symbol | $x’ = \left( \dfrac{x}{60}\right)^{\circ}$ |
| $^{\prime\prime}$ | Arcsecond symbol | $38^{\prime\prime} = \left(\dfrac{38}{60}\right)’$ |
| ∟ | Right angle symbol | 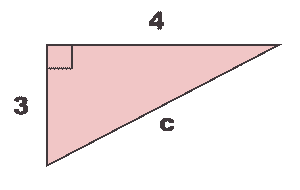 |
| $-, =, \equiv$ (hatch marks) | Equal angle/length | 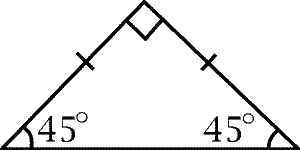 |
Circle-related Symbols
A circle can be thought of as a set of all points equidistant to a given point, and often plays a crucial role in the development of Euclidean geometry and trigonometry. The following table documents some of the most notable symbols related to circle — along their respective meaning and example.
| Symbol Name | Explanation | Example |
|---|---|---|
| $O$ | Variable for circle (or center of circle) | If circles $O_1$ and $O_2$ share the same radius, then they are congruent. |
| $\odot P$ | Circle centered around point $P$ | If $P \ne Q$, then $\odot P \ne \odot Q$. |
| $r$ | Radius of circle | $r = \sqrt{\dfrac{A}{\pi}}$ |
| $d$ | Diameter of circle | $d =2r$ |
| $C$ | Circumference of circle | $C=2\pi r$ |
| $\overparen{AB}$ | Arc segment between points $A$ and $B$ | If $\overline{AB}$ is a diameter, then $\overparen{AB}$ would correspond to the half-circumference. |
| $\pi$ | Pi (Archimedes’ constant) | $\pi = \dfrac{C}{d} \approx 3.1416$ |
| $\tau$ | Tau (constant representing the ratio between circumference and radius) | $\tau = 2 \pi \approx 6.2832$ |
| $A$ | Area of a circle | $A \propto r^2$ |
Trigonometric Functions
In trigonometry, many functions are used to relate angles within a right triangle to its various lengths or ratios. The following table documents some of the most common functions in this category — along with their respective usage and example.
| Symbol Name | Explanation | Example |
|---|---|---|
| $\sin \theta$ | Sine function | $\sin\left(\dfrac{\pi}{2}\right) = 1$ |
| $\mathrm{crd}\, \theta$ | Chord function (Length of chord subtended by angle $\theta$ in unit circle) | $\mathrm{crd}\, \theta \ge \sin \theta$ |
| $\cos \theta$ | Cosine function | $\sin^2 \theta + \cos^2 \theta =1$ |
| $\tan \theta$ | Tangent function | $\tan \theta = \dfrac{\sin \theta}{\cos \theta}$ |
| $\csc \theta$ | Cosecant function | $\csc \theta = \dfrac{1}{\sin \theta}$ |
| $\sec \theta$ | Secant function | $\sec^2 \theta = \tan^2 \theta + 1$ |
| $\cot \theta$ | Cotangent function | $\cot \theta = \dfrac{\cos \theta}{\sin \theta}$ |
| $\arcsin x$, $\sin^{-1}x$ | Arcsine function (Inverse sine) | $-\dfrac{\pi}{2} \le \arcsin x \le \dfrac{\pi}{2}$ |
| $\arccos x$, $\cos^{-1}x$ | Arccosine function (Inverse cosine) | $\arccos \left( \dfrac{\sqrt{2}}{2} \right) = \dfrac{\pi}{4}$ |
| $\arctan x$, $\tan^{-1}x$ | Arctangent function (Inverse tangent) | $\displaystyle \lim_{x \to \infty} \arctan x = \dfrac{\pi}{2}$ |
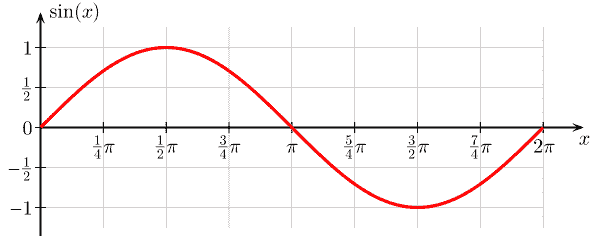
Sine function 
Cosine function 
Tangent function 
Cosecant function 
Secant function 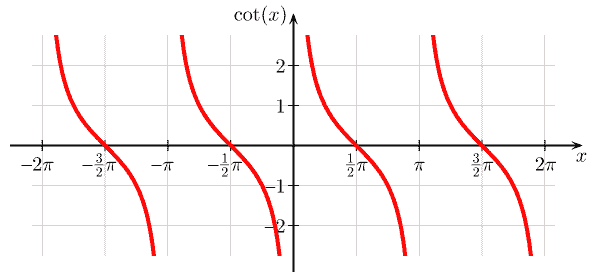
Cotangent function
Other 2D/3D-figure-related Symbols
In elementary geometry, much of the study revolves around the analysis of polygons, polyhedra and other 3-dimensional figures. The following table documents some of the most notable symbols in these categories — along with each symbol’s respective meaning and usage.
| Symbol Name | Explanation | Example |
|---|---|---|
| $\triangle ABC$ | Triangle with vertices $A$, $B$ and $C$ | $\triangle ABC \sim \triangle A’B’C’$ |
| $\square ABCD$ | Square/Quadrilaterals with vertices $A$, $B$, $C$ and $D$ | If $\overline{AB} \parallel \overline{CD}$, then $\square ABCD$ is a trapezoid. |
| $\Pi$ (Capital pi) | Variable for planes | $\Pi_1 \parallel \Pi_2$ |
| $F \sim F’$ | Figure $F$ is similar to figure $F’$ | $\triangle ABC \sim \triangle PQR$ |
| $F \nsim F’$ | Figure $F$ is not similar to figure $F’$ | Since $F$ is a regular pentagon and $F’$ is not, $F \nsim F’$. |
| $F \cong F’$ | Figure $F$ is congruent to figure $F’$ | $\triangle ABC \cong \triangle A’B’C’$ $\implies \overline{AB} \cong \overline{A’B’}$ |
| $F \ncong F’$ | Figure $F$ is not congruent to figure $F’$ | $\square ABCD \nsim \\ \square A’B’C’D’ \implies \\ \square ABCD \ncong \\ \square A’B’C’D’ $ |
| $\varphi$ (phi) | Golden ratio | $\varphi = \dfrac{1 + \sqrt{5}}{2} \approx 1.618$ |
| $h$ | Height of triangle/quadrilateral/ 3D figures | Since $h = 5$, $A=\dfrac{5 \cdot 3}{2}$. |
| $b$ | Base of triangle/quadrilateral | For an obtuse triangle, $b$ corresponds to the extended base of the triangle. |
| $l$ | Length of rectangle/rectangular solid | When $l=10$, $A= 10 \cdot 20$. |
| $w$ | Width of rectangle/rectangular solid | $A = lw$ |
| $P$ | Perimeter of planar figure | For a rectangle, $P = 2l + 2w$. |
| $A$ | Area of planar figure (or surface area of 3D figure) | For a triangle, $A = \dfrac{bh}{2}$. |
| $V$ | Volume of 3D figure | For a sphere, $V \propto r^3$. |
| $n$ | Number of sides in polygon | For an $n$-gon, the sum of interior angles equals $(n – 2) \cdot 180^{\circ}$. |
| $V$ | Number of vertices in polyhedron | For a cube, $V = 8$. |
| $E$ | Number of edges in polyhedron | In general, $E \ge V$ for polyhedra. |
| $F$ | Number of faces in polyhedron | For a tetrahedron, $F=4$. |
| $\chi$ (chi) | Euler characteristic | For convex polyhedra, $\chi = V-E + F = \\ 2.$ |
The following figures illustrate the 5 platonic solids (regular, convex polyhedra), along with their respective number of vertices, edges and faces.

Tetrahedron $(V= 4, E= 6, \\ F=4, \chi=2)$ 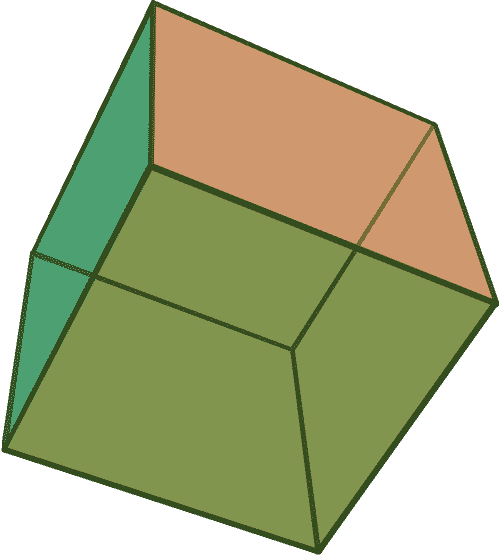
Cube $(V=8, E=12, \\ F=6, \chi=2)$ 
Octahedron $(V=6, E=12, \\ F=8, \chi=2)$ 
Dodecahedron $(V=20, E=30, F=12, \chi= 2)$ 
Icosahedron $(V=12, E=30, F=20, \chi=2)$
For the master list of symbols, see mathematical symbols. For lists of symbols categorized by type and subject, refer to the relevant pages below for more.
- Arithmetic and Common Math Symbols
- Geometry and Trigonometry Symbols
- Logic Symbols
- Set Theory Symbols
- Greek, Hebrew, Latin-based Symbols
- Algebra Symbols
- Probability and Statistics Symbols
- Calculus and Analysis Symbols

Prefer the PDF version instead?
Get the master summary of mathematical symbols in eBook form — along with each symbol’s usage and LaTeX code.
Additional Resources
- Definitive Guide to Learning Higher Mathematics: A standalone, 10-principle framework for tackling higher mathematical learning, thinking and problem solving efficiently
- Ultimate LaTeX Reference Guide: Definitive reference guide to make the LaTeXing process more efficient and less painful
- 10 Commandments of Higher Mathematical Learning: An illustrated web guide on 10 scalable rules for learning higher mathematics
- Definitive Glossary of Higher Math Jargon: A tour around higher mathematics in 106 terms


Wonderfully Dealt with.
Hi Deb. Glad you like it!
In trigonometry, we mostly study the relationships between the side lengths and angles of a right-angle triangle. There are six trigonometric relations.
Hi GG. Great remark!