Set theory is a branch of mathematics dedicated to the study of collections of objects, its properties, and the relationship between them. The following list documents some of the most notable symbols in set theory, along each symbol’s usage and meaning.
For readability purpose, these symbols are categorized by their function into tables. Other comprehensive lists of symbols — as categorized by subject and type — can be also found in the relevant pages below (or in the navigational panel).
Table of Contents

Prefer the PDF version instead?
Get the master summary of mathematical symbols in eBook form — along with each symbol’s usage and LaTeX code.
Constants
In set theory, constants are often one-character symbols used to denote key mathematical sets. The following table documents the most notable of these — along with their respective meaning and example.
| Symbol Name | Explanation | Example |
|---|---|---|
| $\varnothing$, $\emptyset$, $\{ \}$ | Empty set | $|\varnothing|=0$ |
| $\mathbb{N}$ | Set of natural numbers | $1 \in \mathbb{N}$ |
| $\mathbb{Z}$ | Set of integers | If $m, n \in \mathbb{Z}$, then $m+n, mn \in \mathbb{Z}$. |
| $\mathbb{Q}$ | Set of rational numbers | $\pi \notin \mathbb{Q}$ |
| $\mathbb{R}$ | Set of real numbers | $e \in \mathbb{R}$ |
| $\mathbb{C}$ | Set of complex numbers | $\mathbb{N} \subseteq \mathbb{Z} \subseteq \mathbb{Q} \subseteq \mathbb{R} \subseteq \mathbb{C}$ |
| $\mathbb{U}, U$ | Universal set | When $U = \mathbb{R}$, $\overline{\mathbb{Q}} = \mathbb{R} \setminus \mathbb{Q}$. |
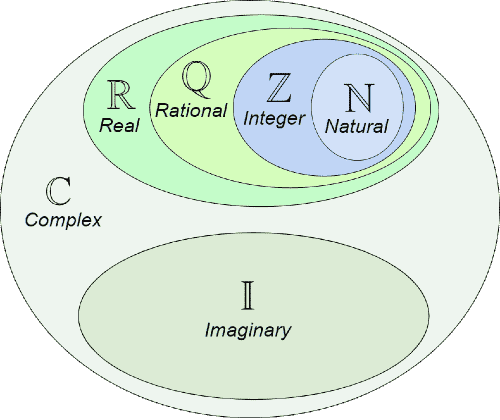
For other key sets of numbers, see key mathematical sets in algebra.
Variables
Similar to other fields in mathematics, set theory often uses a designated list of variable symbols to refer to varying objects and quantities. The following table documents the most common of these — along with their respective example and meaning.
| Symbol Name | Used For | Example |
|---|---|---|
| $A ,B, C$ | Sets | $A \subseteq B \cup C$ |
| $a, b, c$ | Elements of set | If $a \in A$ and $b \in B$, then $a, b \in A \cup B$. |
| $\alpha, \beta, \gamma$ | Ordinal numbers | If $P(\beta)$ for all $\beta < \alpha$ implies $P(\alpha)$, for all $\alpha$, then $P$ holds in general by transfinite induction. |
| $\lambda$ | Limit ordinals | $\lambda$ is a limit ordinal if it’s neither $0$ nor a successor ordinal. |
| $\kappa$ | Cardinal numbers | For each finite cardinal $\kappa$, its successor is simply $\kappa + 1$. |
Delimiters
In set theory, delimiters are symbols used to delineate the separation between independent mathematical entities, and often occur in the context of definition of sets. The following table documents the most common of these — along with their respective usage and meaning.
| Symbol Name | Explanation | Example |
|---|---|---|
| $\{ \}$ | Indicator for sets | $\{5, e, \pi, 1\}$ |
| $( )$ | Indicator for tuples | $(1, 2.89) \in \mathbb{N} \times \mathbb{R}$ |
| $|, :$ | ‘Such that’ marker in set-builder notation | $\{ x^2 : x \in \mathbb{Z} \} =$ $\{ y \in \mathbb{Z} \mid y = x^2$ $\mathrm{for \ some \ } x \in \mathbb{Z} \} $ |
Operators
Since the concept of set lies at the foundation of mathematics, many set operators — which allow one to refer to new sets through pre-existing sets — exist. The following table documents the most notable of these — along with their respective example and meaning.
| Symbol Name | Explanation | Example |
|---|---|---|
| $\overline{A}, A^{\mathrm{c}}, A’$ | Complement of set $A$ | $\overline{A} = \{ x \in U \mid \\ x \notin A \}$ |
| $A \cap B$ | Intersection of sets $A$ and $B$ | $\mathbb{R} \cap \mathbb{I} = \{ 0 \}$ |
| $\displaystyle \bigcap_{i=m}^n A_i$, $\, \displaystyle \bigcap_{i \in I} A_i$ | Generalized intersection of sets $A_i$ | $\displaystyle \bigcap_{i=1}^{\infty} \, ( 0, 1 / i ) = \varnothing$ |
| $A \cup B$ | Union of sets $A$ and $B$ | $A \cup (B \cup C) =$ $(A \cup B) \cup C$ |
| $\displaystyle \bigcup_{i=m}^n A_i$, $\, \displaystyle \bigcup_{i \in I} A_i$ | Generalized union of sets $A_i$ | $\displaystyle \bigcup_{i=\{3, 5 , 8\}} [-i, i] = [-8, 8]$ |
| $A \sqcup B$ | Disjoint union of sets $A$ and $B$ | If $A = \{ 2, 5 \}$ and $B = \{ 1 ,2 \}$, then $A \sqcup B = \{ (2, a), (5, a),$ $(1,b), (2,b) \}.$ |
| $\displaystyle \bigsqcup_{i=m}^n A_i$, $\, \displaystyle \bigsqcup_{i \in I} A_i$ | Generalized disjoint union of sets $A_i$ | $\displaystyle \bigsqcup_{i=1}^n A_i = \bigcup_{i=1}^n$ $\{ (a_i, i) \mid a_i \in A_i \}$ |
| $A \setminus B$, $A-B$ | Set difference ($A$ minus $B$) | $\{ 5, 6 ,8\} \setminus \{6, 9\} =$ $\{5, 8\}$ |
| $A \, \triangle \, B$, $A \ominus B$ | Symmetric difference of sets $A$ and $B$ | $A \, \triangle \, B =$ $(A \setminus B) \cup (B \setminus A)$ |
| $A \times B$ | Cartesian product ($A$ times $B$) | In general, $A \times B \ne B \times A$. |
| $A^n$ | $n$th Cartesian power of set $A$ | $\mathbb{R}^3 = \mathbb{R} \times \mathbb{R} \times \mathbb{R}$ |
| $\displaystyle \prod_{i=m}^n A_i$ | Generalized Cartesian product of sets $A_i$ | $\displaystyle \prod_{i=1}^n \{i\} = \{ (1, \ldots, n) \}$ |
| $\mathcal{P}(A)$ | Power set of $A$ | $\mathcal{P}(\{a, b\}) =$ $\left\{ \varnothing, \{a\}, \{b\}, \{a, b\} \right\}$ |
| $2^{A}$ | Set of functions from $A$ to a two-element set | For all sets $A$, $|2^A| = |\mathcal{P}(A)$|. |
| $B^A$ | Set of functions from $A$ to $B$ | For all finite sets $A$ and $B$, $|B^A| = |B|^{|A|}$. |
The following diagrams, known as Venn diagrams, provide a visualization of five of the key sets mentioned above (where $A$ and $B$ are represented by the left and the right circle, respectively).
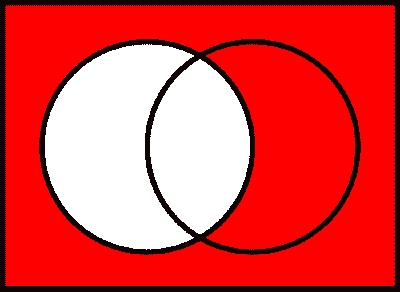
$\overline{A}$ 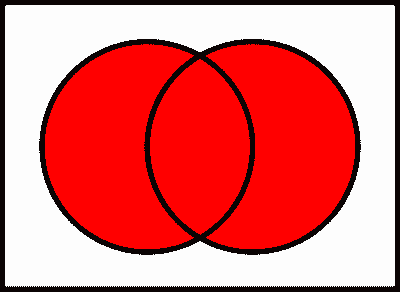
$A \cup B$ 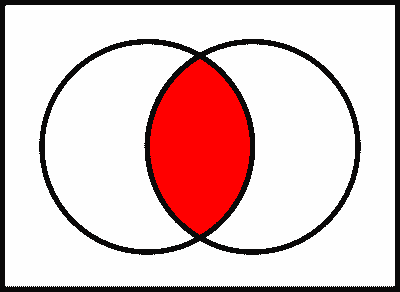
$A \cap B$ 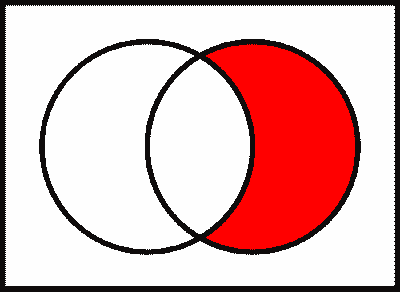
$B \setminus A$ 
$A \, \triangle \, B$
Relational Symbols
In set theory, relational symbols are often used to describe relationships between sets, or relationships between a set and its element. The following table documents the most notable of these symbols — along with their respective meaning and example.
| Symbol Name | Explanation | Example |
|---|---|---|
| $x \in A$ | Set membership (Element $x$ is in set $A$) | $i \in \mathbb{C}$ |
| $x \notin A$ | Set non-membership (Element $x$ is not in set $A$) | $\pi \notin \mathbb{Q}$ |
| $A \ni x$ | Set inclusion (Set $A$ includes element $x$) | $A \ni x \iff x \in A$ |
| $A \not\ni x$ | Set non-inclusion (Set $A$ does not include element $x$) | $\{a\} \not\ni \{a\}$ |
| $A = B$ | Set equivalence (Sets $A$ and $B$ are equal) | $\varnothing = \{ \}$ |
| $A \subseteq B$ | Subset relation ($A$ is a subset of $B$) | $\mathbb{N} \subseteq \mathbb{Q}$ |
| $A \subset B$ | Proper subset relation ($A$ is a proper subset of $B$) | $A \subset B \iff$ $A \subseteq B \ \mathrm{and}\ A \ne B$ |
| $A \not\subseteq B$ | Non-subset relation ($A$ is not a subset of $B$) | If $A \not\subseteq B$, then there exists an $x \in A$ such that $x \notin B$. |
| $A \supseteq B$ | Superset relation ($A$ is a superset of $B$) | $\{5, 8, 1\} \supseteq \{1, 8\}$ |
| $A \supset B$ | Proper superset relation ($A$ is a proper superset of $B$) | $A \supset B \iff \\ B \subset A$ |
| $A \not\supseteq B$ | Non-superset relation ($A$ is not a superset of $B$) | $\mathbb{N} \not\supseteq \mathbb{R}$ |
Cardinality-related Symbols
In set theory, the concept of cardinality provides a way of quantifying and comparing the sizes of different sets. The following table documents some of the most notable symbols related to cardinality — along with each symbol’s usage and meaning.
(For a refresher on Greek and Hebrew symbols, see Greek, Hebrew and Latin-based symbols.)
| Symbol Name | Explanation | Example |
|---|---|---|
| $|A|$ | Cardinality of set $A$ | $|\mathbb{N}|=|\mathbb{Z}|$ |
| $\aleph_0$, $\aleph_1, \ldots$ | Aleph numbers | Under continuum hypothesis, $\aleph_1 = 2^{\aleph_0}$. |
| $\beth_0, \beth_1, \ldots$ | Beth numbers | $\beth_0 = |\mathbb{N}|,$ $\beth_1=|\mathcal{P}(\mathbb{N})|,$ $\beth_2 = |\mathcal{P}(\mathcal{P}(\mathbb{N}))|$ |
| $\gimel$ | Gimel function | $\gimel(\kappa) > \kappa$ |
| $\mathfrak{c}$ | Cardinality of the continuum | $|\mathbb{R}| = \mathfrak{c} = |\mathbb{\mathcal{P}(\mathbb{N})}|$ |
| $\omega_0, \omega_1, \ldots$ | Omega ordinals | $\omega = \{ 0, 1, 2, \ldots \},$ $\omega + 1 = \omega \cup \{ \omega \}$ |
| $\Omega$ | First uncountable ordinal | $\Omega = \omega_1$ |
| $\varepsilon_0, \varepsilon_1, \ldots$ | Epsilon ordinals | $\varepsilon_0 = \omega^{\omega^{\omega^{\ \cdot^{\,\cdot^{\,\cdot}}}}}$ |
| $S(\alpha)$ | Successor of ordinal $\alpha$ | $\alpha + S(\beta) = \\ S (\alpha + \beta)$ |
| $\kappa^+$ | Successor of cardinal $\kappa$ | $\aleph_{\alpha}^+ = \aleph_{\alpha+1}$ |
For the master list of symbols, see mathematical symbols. For lists of symbols categorized by type and subject, refer to the relevant pages below for more.
- Arithmetic and Common Math Symbols
- Geometry and Trigonometry Symbols
- Logic Symbols
- Set Theory Symbols
- Greek, Hebrew, Latin-based Symbols
- Algebra Symbols
- Probability and Statistics Symbols
- Calculus and Analysis Symbols

Prefer the PDF version instead?
Get the master summary of mathematical symbols in eBook form — along with each symbol’s usage and LaTeX code.
Additional Resources
- Definitive Guide to Learning Higher Mathematics: A standalone, 10-principle framework for tackling higher mathematical learning, thinking and problem solving efficiently
- Ultimate LaTeX Reference Guide: Definitive reference guide to make the LaTeXing process more efficient and less painful
- 10 Commandments of Higher Math Learning: Illustrated web guide on the 10 principles that make higher mathematical learning more efficient and more meaningful
- Definitive Glossary of Higher Math Jargon: A tour around higher mathematics in 106 terms


The best and most objective resume of symbols used by those who are working on the subject of transfinite numbers and and their practical functions
Hi Noenio. Glad you find it useful!
This resource site is an amazing source of information and I’m glad I found it!
Hi Beylikdüzü. Glad you like it!
Your blog sparks a sense of curiosity and encourages readers to explore new ideas.
Hi Reklam. Glad you like it!