The language and vocabulary of mathematics contain a large amount of symbols — some being more technical than others. Like letters in the alphabet, they can be used to form words, phrases and sentences that would constitute a larger part of the mathematical lexicon. \[ \begin{gather*}x \longrightarrow x+1 \longrightarrow (x+1)^2 \longrightarrow (x+1)^2 \ge 0 \\ \longrightarrow \forall x \in \mathbb{R} [ (x+1)^2 \ge 0 ] \end{gather*} \] A math symbol can be used for different purposes from one mathematical subfield to another (e.g., $\sim$ as logical negation and similarity of triangle), just as multiple symbols can be used to delineate the same concept or relation (e.g., $\times$ and $\cdot$ in multiplication).
A basic understanding about mathematical terminology is essential to a solid foundation in higher mathematics. To that end, the following is a compilation of some of the most well-adapted, commonly-used symbols in mathematics.
Moreover, these symbols are further categorized by their function into tables. More comprehensive lists of symbols — as categorized by subject and type — can be also found in the relevant pages below (or in the navigational panel).
Table of Contents

Prefer the PDF version instead?
Get the complete, comprehensive list of mathematical symbols in eBook form — along with each symbol’s usage and LaTeX code.
Constants
In mathematics, constants are symbols that are used to refer to non-varying objects. These can include key numbers, key mathematical sets, key mathematical infinities and other key mathematical objects (such as the identity matrix $I$).
Mathematical constants often take form of an alphabet letter — or a derivative of it. In some occasions, a constant might be regarded as a variable in the larger context. The following tables feature some of the most commonly-used constants, along with their name, meaning and usage.
Key Mathematical Numbers
| Symbol Name | Explanation | Example |
|---|---|---|
| $0$ (Zero) | Additive identity of common numbers | $3 + 0 =3$ |
| $1$ (One) | Multiplicative identity of common numbers | $5 \times 1 = 5$ |
| $\sqrt{2}$ (Square root of $2$) | Positive number whose square is $2$. Approximately $1.41421$. | $(\sqrt{2} + 1)^2 = 3 + 2\sqrt{2}$ |
| $e$ (Euler’s constant) | Base of the natural logarithm. Limit of the sequence $(1+\frac{1}{n})^n$. Approximately $2.71828$. | $\ln (e^2) = 2 $ |
| $\pi$ (Pi, Archimedes’ constant) | Ratio of a circle’s circumference to its diameter. Half-circumference of a unit circle. Approximately $3.14159$. | $\dfrac{\pi^2}{6} = \dfrac{1}{1^2} + \dfrac{1}{2^2} + \cdots$ |
| $\varphi$ (Phi, golden ratio) | Ratio between a larger number $a$ and a smaller number $b$ when $\frac{a+b}{a} = \frac{a}{b}$. Positive solution to the equation $x^2-x-1 = 0$. | $\varphi = \dfrac{1+\sqrt{5}}{2} \approx 1.61803$ |
| $i$ (Imaginary unit) | The principal root of $-1$. Foundational component of a complex number. | $(1+i)^2 = 2i$ |
Key Mathematical Sets
For a more comprehensive list, see key mathematical sets in algebra.
| Symbol Name | Explanation | Example |
|---|---|---|
| $\varnothing$ (Empty set) | Set with no element | $|\varnothing| = 0$ |
| $\mathbb{N}$ (N) | Set of natural numbers | $\forall x, y \in \mathbb{N}$, $x+y \in \mathbb{N}$ |
| $\mathbb{Z}$ (Z) | Set of integers (Z stands for zahlen, number in German) | $ \mathbb{N} \subseteq \mathbb{Z}$ |
| $\mathbb{Z}_+$ (Z-plus) | Set of positive integers | $3 \in \mathbb{Z}_+$ |
| $\mathbb{Q}$ (Q) | Set of rational numbers (Q stands for quotient) | $\sqrt{2} \notin \mathbb{Q}$ |
| $\mathbb{R}$ (R) | Set of real numbers | $\forall x \in \mathbb{R}, x^2 \ge 0$ |
| $\mathbb{R}_+$ (R-plus) | Set of positive real numbers | $\forall x,y \in \mathbb{R}_+$, $xy \in \mathbb{R}_+$ |
| $\mathbb{C}$ (C) | Set of complex numbers | $\exists z \in \mathbb{C}\, (z^2 + 1 =0)$ |
| $\mathbb{Z}_n$ (Z-n) | Set of integers modulo $n$ | In the world of $\mathbb{Z}_2$, $1+1=0$. |
| $\mathbb{R}^3$ (R-three) | Three-dimensional Euclidean space | $(5, 1, 2) \in \mathbb{R}^3$ |
Key Mathematical Infinities
In mathematics, many different types of infinity exist. These include the purely notational use of the lemniscate symbol ($\infty$), and the use of the following symbols in the context of cardinal/ordinal infinities:
| Symbol Name | Explanation | Example |
|---|---|---|
| $\aleph_0$ (Aleph-naught) | Cardinality of the set of natural numbers | $\aleph_0 + 5 = \aleph_0$ |
| $\mathfrak{c}$ (Continuum) | Cardinality of the set of real numbers | $\mathfrak{c}=2^{\aleph_0}$ |
| $\omega$ (Omega) | Smallest infinite ordinal number | $\forall n \in \mathbb{N}, n < \omega$ |
For a more comprehensive list, see cardinality-related symbols.
Other Key Mathematical Objects
| Symbol Name | Explanation | Example |
|---|---|---|
| $\mathbf{0}$ (Zero) | Zero vector of a vector space | $\forall \mathbb{v} \in V$, $\mathbf{v} + \mathbf{0} = \mathbf{v}$ |
| $e$ (E) | Identity element of a group | $e \circ e = e$ |
| $I$ (I) | Identity matrix | $AI = IA = A$ |
| $C$ (C) | Constant of integration | $\displaystyle \int 1 \, \mathrm{d}x =$ $x + C$ |
| $\top$ (Tautology) | A sentence in formal logic which is unconditionally true | For each proposition $P$, $P \land \top \equiv P$. |
| $\bot$ (Contradiction) | A sentence in formal logic which is unconditionally false | For each proposition $P$, $P \land \lnot P \equiv \bot.$ |
| $Z$ (Z) | Standard normal distribution | $Z \sim N(0,1)$ |
Variables
A mathematical variable is a symbol that functions as a placeholder for varying expressions or quantities. The same variable can be used on a repeated basis to refer to the same thing — or quantified to form sentences that have a more definite meaning: \begin{gather*}x, y \longrightarrow x + e^x = y \longrightarrow \exists y \in \mathbb{R}\, (x + e^x = y) \\ \longrightarrow \forall x \in \mathbb{R} \, \exists y \in \mathbb{R}\, (x + e^x = y) \end{gather*} In some cases, variables can be thought of as constants in narrower contexts (e.g., as parameters), while in other cases, variables are used in conjunction with subscripts to make up for the lack of letters (e.g., $x_3$).
While variables in mathematics are often used to represent numbers, they can also be used to represent other objects such as vectors, functions and matrices. The following tables document some of the most common conventions for variables — along with the context where they are adopted and used.
Variables for Numbers
| Symbol(s) | Used For | Example |
|---|---|---|
| $m, n, p, q$ | Integers and natural numbers | If $mn$ is odd, then both $m$ and $n$ are odd. |
| $a, b, c$ | Coefficients of functions and equations | A line of the form $ax+by=0$ passes through the origin. |
| $x, y, z$ | Unknowns in functions and equations | If $2x + 5= 3$, then $x=-1$. |
| $\Delta$ | Discriminant | $\Delta = b^2 – 4ac$ for quadratic polynomials |
| $i, j, k$ | Index variables in summations and products | $\sum _{i=1}^{10} i = 55$ |
| $t$ | Time | At $t=5$, the velocity is $v(5)=32$. |
| $z$ | Complex numbers | $z \overline{z} = |z|^2$ |
Variables in Geometry
For more symbols in geometry and trigonometry, see geometry and trigonometry symbols.
| Symbol(s) | Used For | Example |
|---|---|---|
| $P, Q, R, S$ | Vertices | $\overline{PQ} \perp \overline{QR}$ |
| $\ell$ | Lines | $\ell_1 \parallel \ell_2$ |
| $\alpha, \beta, \gamma, \theta$ | Angles | $\alpha + \beta + \theta = 180^{\circ}$ |
Variables in Calculus
For a more comprehensive list, see constants and variables in calculus.
| Symbol(s) | Used For | Example |
|---|---|---|
| $f(x), g(x,y),h(z)$ | Functions | $f(2) = g(3,1) + 5$ |
| $a_n, b_n, c_n$ | Sequences | $\displaystyle a_ n = \frac{3}{n+2} $ |
| $h, \Delta x$ | Limiting variables in derivatives | $\displaystyle \lim_{h \to 0} \frac{e^{h}-e^{0}}{h} = 1$ |
| $\delta, \varepsilon$ | Small quantities in proofs involving limits | For all $\varepsilon >0$, there is a $\delta >0$ such that $|x|<\delta$ implies $|2x|<\varepsilon$. |
| $F(x), G(x)$ | Antiderivatives | $F(x)’ = f(x)$ |
Variables in Linear Algebra
For a more comprehensive list, see variables in algebra.
| Symbol(s) | Used For | Example |
|---|---|---|
| $\mathbf{u}, \mathbf{v}, \mathbf{w}$ | Vectors | $3\mathbf{u}+4\mathbf{v}=\mathbf{w}$ |
| $A, B, C$ | Matrices | $AX = B$ |
| $\lambda$ | Eigenvalues | $A\mathbf{v}=\lambda \mathbf{v}$ |
Variables in Set Theory and Logic
For more comprehensive lists on the topics, see variables in logic and variables in set theory.
| Symbol(s) | Used For | Example |
|---|---|---|
| $A, B, C$ | Sets | $A \subseteq B \cup C$ |
| $a, b, c$ | Elements | $a \in A$ |
| $P, Q, R$ | Propositions | $P \lor \lnot P \equiv \top$ |
Variables in Probability and Statistics
For a more comprehensive list, see variables in probability and statistics.
| Symbol(s) | Used For | Example |
|---|---|---|
| $X, Y, Z$ | Random variables | $E(X + Y) =$ $E(X) + E(Y)$ |
| $\mu$ | Population means | $H_0\!:\mu = 5$ |
| $\sigma$ | Population standard deviations | $\sigma_1 = \sigma_2$ |
| $s$ | Sample standard deviations | $s \ne \sigma$ |
| $n$ | Sample sizes | If $n\ge 30$, use the normal distribution. |
| $\rho$ | Population correlations | $H_a\!: \rho < 0$ |
| $r$ | Sample correlations | If $r = 0.75$, then $r^2 = 0.5625$. |
| $\pi$ | Population proportions | $\pi = 0.5$ |
| $p$ | Sample proportions | $p = \dfrac{X}{n}$ |
Delimiters
Similar to punctuation marks in English, delimiters are a set of symbols which indicate the boundaries between independent mathematical expressions. They are often used to specify the scope for which an operation or rule would apply, and can occur both as an isolate symbol or as a pair of opposite-looking symbols.
In many scenarios, delimiters are used primarily for grouping purposes. The following table features some of the most commonly-used delimiters, along with their function and usage.
| Symbol(s) | Function | Example |
|---|---|---|
| $.$ | Decimal separator | $25.9703$ |
| $:$ | Ratio indicator | $1:4:9 =$ $3:12:27$ |
| $,$ | Object separator | $(3, 5, 12)$ |
| $(), [], \{\}$ | Order-of-operation indicators | $(a + b) \times c$ |
| $(), []$ | Interval indicators | $3\notin (3,4]$, $4 \in (3,4]$. |
| $(), []$ | Vector/matrix builder | $\begin{pmatrix} 1 & 4 \\ 3 & 6 \end{pmatrix}$ |
| $\{\}$ | Set builder | $\{ \pi, e, i\}$ |
| $|$, $\, :$ | “Such that” markers | $\{ x \in \mathbb{R} \, |\, x^2 – 2 =0 \}$ |
| $| |, \| \|$ | Norm-related operators | $\| (3, 4) \| = 5$ |
| $\begin{cases}\end{cases}$ | Piecewise-function marker | $f(x) = \begin{cases} 1 & x \ge 0 \\ 0 & x < 0 \end{cases}$ |
| $\langle\rangle$ | Inner product operator | $\langle ka, b\rangle = k\langle a, b \rangle$ |
| $\lceil \rceil$ | Ceiling operator | $\lceil 2.476 \rceil = 3$ |
| $\lfloor \rfloor$ | Floor operator | $\lfloor \pi \rfloor = 3$ |
Operators
An operator is a symbol used to denote an operation — a function which takes one or multiple objects to another similar object. Most of the operators are unary and binary in nature (i.e., taking one and two inputs to their intended target, respectively), with the most common ones being the arithmetic operators (e.g., $+$).
Much like the case in English, operators allow one to expand the lexicon of mathematics where only finitely many symbols exist. The following tables feature some of the most commonly-used operators in mathematics — along with their usage and intended meaning.
Common Operators
| Symbol(s) | Explanation | Example |
|---|---|---|
| $x + y$ | Sum of $x$ and $y$ | $2a + 3a =5a$ |
| $x-y$ | Difference of $x$ and $y$ | $11-5=6$ |
| $-x$ | Additive inverse of $x$ | $-3 + 3 =0$ |
| $x \times y$, $x \cdot y$, $xy$ | Product of $x$ and $y$ | $(m+1)n=mn+n$ |
| $\dfrac{1}{x}, x^{-1}$ | Multiplicative inverse/reciprocal of $x$ | $\dfrac{1}{9} \times 9 = 9 \times \dfrac{1}{9} = 1$ |
| $x \div y, x / y$ | Quotient of $x$ over $y$ | $152 \div 3 = 50.\overline{6}$ |
| $\dfrac{x}{y}$ | Fraction ($x$ over $y$) | $\dfrac{53 + 5}{6} =$ $\dfrac{53}{6}+\dfrac{5}{6}$ |
| $x^y$ | $x$ raised to the power of $y$ | $3^4 = 81$ |
| $x \pm y$ | $x$ plus and minus $y$ | $\dfrac{-b \pm \sqrt{\Delta}}{2a}$ |
| $\sqrt{x}$ | Positive square root of $x$ | $\sqrt{2} \approx 1.414$ |
| $|x|$ | Absolute value of $x$ | $|x-3|<5$ |
| $x \%$ | $x$ percent | $x \% \doteq \dfrac{x}{100}$ |
Function-related Operators
For a more comprehensive list, see function-related symbols.
| Symbol | Explanation | Example |
|---|---|---|
| $\operatorname{dom}(f)$ | Domain of function $f$ | If $g(x)=\ln{x}$, then $\operatorname{dom}(g) = \mathbb{R}_+$. |
| $\operatorname{ran}(f)$ | Range of function $f$ | If $h(y)=\sin y$, then it follows that $\operatorname{ran}(h) = [-1,1]$. |
| $f(x)$ | Image of element $x$ under function $f$ | $g(5)=g(4)+3$ |
| $f(X)$ | Image of set $X$ under function $f$ | $f(A \cap B) \subseteq$ $f(A) \cap f(B)$ |
| $f \circ g$ | Composite function ($f$ of $g$) | If $g(3)=5$ and $f(5)=8$, then $(f \circ g)(3) =8$. |
Elementary Functions
For a more comprehensive list, see key functions in algebra.
| Symbol(s) | Explanation | Example |
|---|---|---|
| $k_n x^n + \cdots + k_0 x^0$ | Polynomial with coefficients $k_0, \ldots, k_n$ | Polynomial $x^3+2x^2+3$ has a root in $(-3, -2)$. |
| $e^x, \exp{x}$ | Natural exponential function | $e^{x+y}=e^x \cdot e^y$ |
| $b^x$ | Exponential function with base $b$ | $2^x > x^2$ for large $x$. |
| $\ln x$ | Natural logarithmic function | $\ln (x^2) = 2 \ln{x}$ |
| $\log x$ | Logarithm function of base 10 (or base $e$) | $\log 10000 = 4$ |
| $\log_b x$ | Logarithm function of base $b$ | $\log_2 x = \dfrac{\ln x}{\ln 2}$ |
| $\sin x$ | Sine function | $\sin \pi = 0$ |
| $\cos x$ | Cosine function | $\cos \dfrac{\pi}{4} = \dfrac{\sqrt{2}}{2}$ |
| $\tan x$ | Tangent function | $\tan x = \dfrac{\sin x}{\cos x}$ |
Algebra-related Operators
For a more comprehensive list, see operators in algebra.
| Symbol(s) | Explanation | Example |
|---|---|---|
| $\gcd (x,y)$ | Greatest common factor of $x$ and $y$ | ${\gcd (35,14)=7}$ |
| $\lfloor x \rfloor$ | Floor of $x$ (largest integer smaller or equal to $x$) | $\lfloor 3.6 \rfloor = 3$ |
| $\lceil x \rceil$ | Ceiling of $x$ (smallest integer larger or equal to $x$) | $\lceil \pi \rceil = 4$ |
| $\min (A)$ | Minimum of set $A$ | If $\min (A) = 3$, then $\min(A+5)=8$. |
| $\max (A)$ | Maximum of set $A$ | $\max(A \cup B) \ge \max (A)$ |
| $x\mathrm{\, mod \,} y$ | Remainder of $x$ under modulus $y$ | $36\mathrm{\, mod \,} 5 = 1$ |
| $\sum_{i=m}^n a_i$ | Sum of $a_i$ (where $i$ runs from $m$ to $n$) | $\sum_{i=1}^5 i^2 = 55$ |
| $\prod_{i=m}^n a_i$ | Product of $a_i$ (where $i$ runs from $m$ to $n$) | $\prod_{i=1}^n i = n!$ |
| $[a]$ | Equivalence class of element $a$ | $[a]\doteq \{x \,|\, xRa\}$ |
| $\deg f$ | Degree of polynomial $f$ | $\deg (2x^2 +3x+5)=2$ |
| $\overline{z}$ | Conjugate of complex number $z$ | $\overline{5-8i}=5+8i$ |
| $|z|$ | Absolute value of complex number $z$ | $|e^{\pi i}|=1$ |
| $\operatorname{arg}(z)$ | Arguments of complex number $z$ | $\operatorname{arg}(1+i)= \\[0.3em] \dfrac{\pi}{4} + 2\pi n$ |
Geometry-related Operators
For more symbols in geometry and trigonometry, see geometry and trigonometry symbols.
| Symbol(s) | Explanation | Example |
|---|---|---|
| $\angle ABC$ | Angle formed by vertices $A$, $B$ and $C$ | $\angle ABC = \angle CBA$ |
| $\measuredangle ABC$, $m\angle ABC$ | Measure of angle formed by vertices $A$, $B$ and $C$ | $\measuredangle ABC = \measuredangle A’B’C’$ |
| $\overleftrightarrow{AB}$ | Infinite line formed by points $A$ and $B$ | $\overleftrightarrow{AB}= \\ \overleftrightarrow{BA}$ |
| $\overline{AB}$ | Line segment between points $A$ and $B$ | If $B \ne B’$, then $\overline{AB} \ne \\ \overline{AB’}.$ |
| $\overrightarrow{AB}$ | Ray from point $A$ to point $B$ | $\overrightarrow{AB} \cong \\ \overrightarrow{CD}$ |
| $|AB|$ | Distance between point $A$ and point $B$ | $|AB|<{|A’B’|}$ |
| $\triangle ABC$ | Triangle formed by vertices $A$, $B$ and $C$ | $\triangle ABC \cong \triangle A’B’C’$ |
| $\square ABCD$ | Quadrilateral formed by vertices $A$, $B$, $C$ and $D$ | $\square ABCD = \square DCBA$ |
Logic-related Operators
For a more comprehensive list, see operators in logic.
| Symbol | Explanation | Example |
|---|---|---|
| $\lnot P$ | Negation (not $P$) | $\lnot (1=2)$ |
| $P \land Q$ | Conjunction ($P$ and $Q$) | $P \land Q \equiv$ $Q \land P$ |
| $P \lor Q$ | Disjunction ($P$ or $Q$) | $\pi^e \in \mathbb{Q} \, \lor$ $\pi^e \notin \mathbb{Q}$ |
| $P \to Q$ | Conditional (if $P$, then $Q$) | $P \to Q \equiv$ $(\lnot P \lor Q)$ |
| $P \leftrightarrow Q$ | Biconditional ($P$ if and only if $Q$) | $P \leftrightarrow Q \implies \\ P \to Q$ |
| $\forall \mathbf{x} P(\mathbf{x})$ | Universal statement (for all $\mathbf{x}$, $P(\mathbf{x})$) | $\forall y \in \mathbb{N},$ $y+1 \in \mathbb{N}$ |
| $\exists \mathbf{x} P(\mathbf{x})$ | Existential statement (there exists $\mathbf{x}$ such that $P(\mathbf{x})$) | $\exists z \, {(z^2 = -\pi)}$ |
Set-related Operators
For a more comprehensive list, see operators in set theory.
| Symbol | Explanation | Example |
|---|---|---|
| $\overline{A} $, $A^c$ | Complement of set $A$ | $\overline{\smash{\overline{A}}\vphantom{\bar{A}}}=A$ |
| $A\cap B$ | Intersection of sets $A$ and $B$ | $\{2,5\}\cap {\{1,3\}} = \varnothing$ |
| $A\cup B$ | Union of sets $A$ and $B$ | $\mathbb{Z}\cup\mathbb{N}=\mathbb{Z}$ |
| $A/B$, $A-B$ | Difference of sets $A$ and $B$ | In general, $A-B \ne$ $B-A.$ |
| $A \times B$ | Cartesian product of sets $A$ and $B$ | $(11, -35) \in \mathbb{N} \times \mathbb{Z}$ |
| $\mathcal{P}(A)$ | Power set of set $A$ | $\mathcal{P}(\varnothing)= \{\varnothing \}$ |
| $|A|$ | Cardinality of set $A$ | $|\mathbb{N}|=\aleph_0$ |
Vector-related Operators
For a more comprehensive list, see operators in linear algebra.
| Symbol | Explanation | Example |
|---|---|---|
| $\| \mathbf{v} \|$ | Norm of vector $\mathbf{v}$ | $\| (3,4)\|=5$ |
| $\mathbf{u} \cdot \mathbf{v}$ | Dot product of vectors $\mathbf{u}$ and $\mathbf{v}$ | $\mathbf{u} \cdot \mathbf{u} = \| \mathbf{u}\|^2$ |
| $\mathbf{u} \times \mathbf{v}$ | Cross product of vectors $\mathbf{u}$ and $\mathbf{v}$ | $\mathbf{u} \times \mathbf{u}=\mathbf{0}$ |
| $\operatorname{proj}_{\mathbf{v}}\mathbf{u}$ | Projection of vector $\mathbf{u}$ onto vector$\mathbf{v}$ | $\operatorname{proj}_{(0,1)}(5,4)=$ $(0,4)$ |
| $\operatorname{span}(S)$ | Span of set of vectors $S$ | $\operatorname{span}(\{\mathbf{i},\mathbf{j}\})=\mathbb{R}^2$ |
| $\operatorname{dim}(V)$ | Dimension of vector space $V$ | $\operatorname{dim}(\mathbb{R}^3)=3$ |
Matrix-related Operators
For a more comprehensive list, see operators in linear algebra.
| Symbol(s) | Explanation | Example |
|---|---|---|
| $A+B$ | Sum of matrices $A$ and $B$ | $A + X = B$ |
| $A-B$ | Difference of matrices $A$ and $B$ | In general, $A-B \ne B-A.$ |
| $-A$ | Additive inverse of matrix $A$ | $B+ (-B)=0$ |
| $kA$ | Scalar product of matrix $A$ and number $k$ | $(-1)A=-A$ |
| $AB$ | Product of matrices $A$ and $B$ | $AI=IA=A$ |
| $A^T$ | Transpose of matrix $A$ | $I^T=I$ |
| $A^{-1}$ | Multiplicative inverse of matrix $A$ | $(AB)^{-1}= \\ B^{-1}A^{-1}$ |
| $\operatorname{tr}(A)$ | Trace of square matrix $A$ | $\operatorname{tr}(A^T)=\operatorname{tr}(A)$ |
| $\det(A), |A|$ | Determinant of square matrix $A$ | $\left| \begin{pmatrix} 1 & 4 \\ 3 & 2 \end{pmatrix} \right| = \\ 2-12 = -10$ |
Probability-related Operators
For a more comprehensive list, see operators in probability and statistics.
| Symbol(s) | Explanation | Exampe |
|---|---|---|
| $n!$ | Factorial of $n$ | $4! = 4 \cdot 3 \cdot 2 \cdot 1$ |
| $n P\,r$ | Permutation ($n$ permute $r$) | $5 P\,3=5 \cdot 4 \cdot 3$ |
| $\displaystyle nCr, \binom{n}{r}$ | Combination ($n$ choose $r$) | $\displaystyle \binom{5}{2} = \binom{5}{3}$ |
| $P(E)$ | Probability of event $E$ | $P(A\cup B\cup C) = 0.\overline{3}$ |
| $P(A\,|\,B)$ | Conditional probability of event $A$ given event $B$ | $P(A\,|\,B)=\dfrac{P(A\cap B)}{P(B)}$ |
| $E(X)$ | Expected value of random variable $X$ | $E(X+Y)=$ $E(X)+E(Y)$ |
| $V(X)$ | Variance of random variable $X$ | $V(5X) = 25V(X)$ |
Statistics-related Operators
For a more comprehensive list, see statistical operators.
| Symbol | Explanation | Example |
|---|---|---|
| $\overline{X}$ | Sample mean of data set $X$ | $\overline{3X} = 3 \overline{X}$ |
| $s^2$ | Sample variance | $s^2 = \dfrac{\sum (X – \overline{X})^2}{n -1}$ |
| $\sigma^2$ | Population variance | $\sigma^2 = \dfrac{\sum (X – \mu)^2}{n}$ |
Key Probability Functions and Distributions
For a more comprehensive list, see probability-distribution-related operators.
| Symbol(s) | Explanation | Example |
|---|---|---|
| ${\operatorname{Bin}(n,p)}$ | Binomial distribution with $n$ trials and probability of success $p$ | If $X$ stands for the number of heads in 10 coin tosses, then $X \sim \operatorname{Bin}(10, 0.5)$. |
| $\operatorname{Geo}(p)$ | Geometric distribution with probability of success $p$ | If $Y \sim \operatorname{Geo}(1/5)$, then $E(Y)=5$. |
| $U(a,b)$ | Continuous uniform distribution from $a$ to $b$ | If $X \sim U(3,7)$, then $V(X)=\dfrac{(7-3)^2}{12}$. |
| $N(\mu,\sigma^2)$ | Normal distribution with mean $\mu$ and variance $\sigma^2$ | If $X \sim N(3, 5^2)$, then $\dfrac{X – 3}{5} \sim Z$. |
| $z_{\alpha}$ | Positive Z-score associated with significance level $\alpha$ | $z_{0.05} \approx 1.645$ |
| $t_{\alpha, \nu}$ | Positive t-score associated with significance level $\alpha$ and degree of freedom $\nu$ | $t_{0.05, 1000} \approx z_{0.05}$ |
| $\chi^2_{\alpha, \nu}$ | Chi-squared score associated with significance level $\alpha$ and degree of freedom $\nu$ | $\chi^2_{0.05, 30} \approx 43.77$ |
| $F_{\alpha, \nu_1, \nu_2}$ | F-score associated with significance level $\alpha$ and degrees of freedom $\nu_1$ and $\nu_2$ | $F_{0.05, 20, 20} \approx 2.1242$ |
Calculus-related Operators
For a more comprehensive list, see calculus and analysis symbols.
| Symbol(s) | Explanation | Example |
|---|---|---|
| $\displaystyle \lim_{n \to \infty} a_n$ | Limit of sequence $a_n$ | $\displaystyle \lim_{n \to \infty} \dfrac{n+3}{2n} = \dfrac{1}{2}$ |
| $\displaystyle \lim_{x \to c} f(x)$ | Limit of function $f$ as $x$ tends to $c$ | $\displaystyle \lim_{x \to 3} \frac{\pi\sin x}{2} = \\[0.8em] \displaystyle \frac{\pi}{2}\lim_{x \to 3} \sin x$ |
| $\operatorname{sup}(A)$ | Supremum (least upper bound) of set $A$ | $\operatorname{sup}([ -3,5))=5$ |
| $\operatorname{inf}(A)$ | Infimum (greatest lower bound) of set $A$ | If $\displaystyle B=\left\{\frac{1}{1}, \frac{1}{2}, \ldots\right\}$, then $\operatorname{inf}(B)=0$. |
| $f’, f^{\prime\prime}, f^{\prime\prime\prime}, f^{(n)}$ | First, second, third and $n$th derivative of function $f$ | $\left( \sin x \right)^{\prime\prime\prime} = -\cos (x)$ |
| $\displaystyle \int_a^b f(x)\, \mathrm{d}x$ | Definite integral of function $f$ from $a$ to $b$ | $ \displaystyle \int_0^1 \dfrac{1}{1+x^2}\, \mathrm{d}x = \dfrac{\pi}{4}$ |
| $\displaystyle \int f(x)\,\mathrm{d}x$ | Indefinite integral of function $f$ | $ \displaystyle \int \ln x\,\mathrm{d}x = \\ x\ln x-x+C$ |
| $f_x$ | Partial derivative of multivariate function $f$ with respect to $x$ | If $f(x,y)= x^2 y^3$, then $f_x (x,y) = 2xy^3$. |
Relational Symbols
Relational symbols are used to express mathematical relations between multiple objects. Many relational symbols are binary in nature, in that they take two objects as inputs and turn them into complete, meaningful sentences (as in the case of the inequality symbol $<$).
Since relational symbols form the building blocks of mathematical sentences, they are of foundational importance in mathematics. The following tables document some of the most commonly-used relational symbols — along with their usage and meaning.
Equality-based Relational Symbols
| Symbol(s) | Explanation | Example |
|---|---|---|
| $x = y$ | $x$ and $y$ are equal | $3x-x = 2x$ |
| $x \ne y$ | $x$ and $y$ are non-equal | $2 \ne 3$ |
| $x \approx y$ | $x$ and $y$ are approximately equal | $\pi \approx 3.1416$ |
| $x \sim y$, $xRy$ | $x$ is related to $y$ (as defined by the relation $R$) | $xRy$ if and only if $|x| = |y|$. |
| $x \equiv y$ | $x$ is equivalent/congruent to $y$ | $2 \equiv 101$ in mod $33$ |
| $f \propto g$ | Function $f$ is proportional to function $g$ | $V \propto r^3$ |
Comparison-based Relational Symbols
For a more comprehensive list, see comparison-based relational symbols in algebra.
| Symbol | Explanation | Example |
|---|---|---|
| $x < y$ | $x$ is less than $y$ | $\sin(x) < 3$ |
| $x > y$ | $x$ is greater than $y$ | $\pi > e$ |
| $x \le y$ | $x$ is less than or equal to $y$ | $n! \le n^n$ |
| $x \ge y$ | $x$ is greater than or equal to $y$ | $x^2 \ge 0$ |
Number-related Relational Symbols
| Symbol | Explanation | Example |
|---|---|---|
| $m \mid n$ | Integer $m$ divides integer $n$ | $101 \mid 1111$ |
| $m \perp n$ | Integers $m$ and $n$ are coprime | $31 \perp 97$ |
Geometry-related Relational Symbols
For more symbols in geometry and trigonometry, see geometry and trigonometry symbols.
| Symbol | Explanation | Example |
|---|---|---|
| $\ell_1 \parallel \ell_2$ | Lines $\ell_1$ and $\ell_2$ are parallel | $\overline{PQ} \parallel \overline{RS}$ |
| $\ell_1 \perp \ell_2$ | Lines $\ell_1$ and $\ell_2$ are perpendicular | $\overrightarrow{AB} \perp \overrightarrow{BC}$ |
| $F \sim F’$ | Figure $F$ is similar to figure $F’$ | $\triangle ABC \sim \triangle DEF$ |
| $F \cong F’$ | Figure $F$ is congruent to figure $F’$ | $\square ABCD \cong \square PQRS$ |
Set-related Relational Symbols
For a more comprehensive list, see relational symbols in set theory.
| Symbol | Explanation | Example |
|---|---|---|
| $a \in A$ | Element $a$ is a member of set $A$ | $\dfrac{2}{3} \in \mathbb{R}$ |
| $a \notin A$ | Element $a$ is not a member of set $A$ | $\pi \notin \mathbb{Q}$ |
| $A \subseteq B$ | Set $A$ is a subset of set $B$ | $A \cap B \subseteq A$ |
| $A = B$ | Set $A$ is equal to set $B$ | If $A = B$, then $A \subseteq B$. |
Logic-related Relational Symbols
For a more comprehensive list, see relational symbols in logic.
| Symbol | Explanation | Example |
|---|---|---|
| ${P\! \implies \! Q}$ | Sentence $P$ implies sentence $Q$ | $x$ is even $\implies$ $2$ divides $x$ |
| $P\! \impliedby \! Q$ | Sentence $P$ is implied by sentence $Q$ | $x = 3 \impliedby$ $3x+ 2 =11$ |
| $P\!\iff \!Q,$ $P \equiv Q$ | Sentence $P$ if and only if sentence $Q$ | $x \ne y \iff$ $(x-y)^2 > 0$ |
| $P \therefore Q$ | $P$, therefore $Q$ | $i \in \mathbb{C} \therefore$ $\exists z\, (z \in \mathbb{C})$ |
| $P \because Q$ | $P$, because $Q$ | $x=\dfrac{\pi}{2} \because$ $\sin x = 1$ and $\cos x =0$ |
Probability-related Relational Symbols
For a more comprehensive list, see relational symbols in probability and statistics.
| Symbol | Explanation | Example |
|---|---|---|
| $A \perp B$ | Events $A$ and $B$ are independent | Since $A \perp B$, we have that $P(A \cap B) = P(A)P(B).$ |
| $X \sim F$ | Random variable $X$ follows distribution $F$ | $Y \sim \operatorname{Bin}(30, 0.4)$ |
Calculus-related Relational Symbols
For a more comprehensive list, see relational symbols in asymptotic analysis.
| Symbol | Explanation | Example |
|---|---|---|
| $f(x) \sim g(x)$ | Function $f$ is asymptotically equal to function $g$ | $\pi(x) \sim \dfrac{x}{\ln x}$ |
| $f(x) \in O(g(x))$ | Function $f$ is in the big-O of $g$ ($f$ “grows at most as fast” as $g$) | $2x^2 + 3x + 3 \in O(x^2)$ |
Notational Symbols
A notational symbol is a convention or shorthand whose role is different from that of a constant, variable, delimiter, operator or relational symbol. It often simply delineates the notational system being used, and might even refer to concepts that have little bearing to any definite mathematical object (e.g., $\infty$).
Common Notational Symbols
| Symbol(s) | Explanation | Example |
|---|---|---|
| $\ldots, \cdots$ | Horizontal ellipsis symbols to indicate a definite, unlisted pattern | $1^2 + 2^2 + \cdots + n^2$ |
| $\vdots, \ddots$ | Vertical ellipsis symbols to indicate a definite, unlisted pattern | $\left( \begin{smallmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mn}\end{smallmatrix}\right)$ |
| $f\!: A \to B$, $A \overset{f}{\to} B$ | Function $f$ with domain $A$ and codomain $B$ | A function $g: \mathbb{N} \to \mathbb{R}$ can be thought of as a sequence. |
| $x \mapsto f(x)$ | Function rule mapping element $x$ to $f(x)$ | The function $x \mapsto x^2$ is increasing in the interval $[0, \infty)$. |
| ${Q.E.D.}, \square, \blacksquare$ | End-of-the-proof symbol | Thus the result is established as desired. $\,\blacksquare$ |
| $Q.E.A.$, ⨳ , ※ | Contradiction symbol | Multiplying both sides of the equation yields that $1=2$. ※ |
Notational Symbols in Geometry and Trigonometry
For more symbols in geometry and trigonometry, see geometry and trigonometry symbols.
| Symbol | Explanation | Example |
|---|---|---|
| $^{\circ}$ | Degree symbol | $\cos(90^{\circ}) = 0$ |
| $’$ | Arcminute symbol | $35^{\prime} = \dfrac{35}{60}$ degrees |
| $^{\prime\prime}$ | Arcsecond symbol | $20^{\prime\prime} = \left( \dfrac{20}{60} \right) ^{\prime}$ |
| $\mathrm{rad}$ | Radian | $\pi \mathrm{\, rad} = 180^{\circ}$ |
| $\mathrm{grad}$ | Gradian | $100 \mathrm{\, grad} = 90^{\circ}$ |
| ∟ | Right angle | 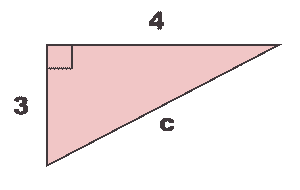 |
| $-$, $=$, $\equiv$ | Equal angle/length | 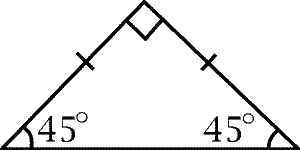 |
Notational Symbols in Calculus
For more symbols in calculus, see calculus and analysis symbols.
| Symbol | Explanation | Example |
|---|---|---|
| $+\infty$ | Positive infinity | $\left(\dfrac{n^2 +1}{n}\right) \to +\infty$ |
| $-\infty$ | Negative infinity | $\displaystyle \lim_{x \to -\infty} e^x =0$ |
| $\Delta \mathbf{x}$ | Change in variable $\mathbf{x}$ | $m = \dfrac{\Delta y}{\Delta x}$ |
| $\mathrm{d} \mathbf{x}$ | Differential of variable $\mathbf{x}$ | $\mathrm{d}y = f'(x)\, \mathrm{d}x$ |
| $\partial \mathbf{x}$ | Partial differential of variable $\mathbf{x}$ | $\dfrac{\partial f}{\partial x}\,\mathrm{d} x$ |
| $\mathrm{d} \mathbf{f}$ | Total differential of multivariate function $\mathbf{f}$ | $\mathrm{d} g(x,y) = \\ \dfrac{\partial g}{\partial x}\,\mathrm{d}x + \dfrac{\partial g}{\partial y}\,\mathrm{d}y$ |
Notational Symbols in Probability and Statistics
For a more comprehensive list, see notational symbols in probability and statistics.
| Symbol | Explanation | Example |
|---|---|---|
| i.i.d. | Independent and identically distributed | Given $n$ i.i.d. random variables $X_1, \ldots, X_n$, $V(X_1 + \cdots + X_n) =$ $V(X_1) + \cdots + V(X_n).$ |
| $H_0$ | Null hypothesis | $H_0\!: \mu = 23$ |
| $H_a$ | Alternative hypothesis | $H_a\!: \sigma_1^2 \ne \sigma_2^2$ |
For lists of symbols categorized by type and subject, refer to the relevant pages below for more.
- Arithmetic and Common Math Symbols
- Geometry and Trigonometry Symbols
- Logic Symbols
- Set Theory Symbols
- Greek, Hebrew, Latin-based Symbols
- Algebra Symbols
- Probability and Statistics Symbols
- Calculus and Analysis Symbols

Prefer the PDF version instead?
Get the master summary of mathematical symbols in eBook form — along with each symbol’s usage and LaTeX code.
Additional Resources
- Ultimate LaTeX Reference Guide: A definitive reference guide for users of LaTeX
- Definitive Guide to Learning Higher Mathematics: A 10-principle framework for tackling higher mathematical learning, thinking and problem solving
- 10 Commandments of Higher Mathematical Learning: An illustrated web guide on 10 scalable rules for learning higher mathematics
- Definitive Glossary of Higher Mathematical Jargon: A tour around higher mathematics in 100 terms


exemplary Reading Stuff Of Very High Standard on the Subject Matter under consideration! Highly Appreciable Work By Math Vault!!
Thank you. More coming soon!
where have you been all of my life …
Hi Jay. Yes we’re a bit late to the game when it comes to mathematical symbols, but we’re getting there!
The d in the notation for differentials (e.g., dx) should be in math italics.
Hi Robert. Yes we were well aware of the roman/italic ‘d’ notations when choosing our typography. Technically, the roman ‘d’ is more correct since ‘d’ is not a variable, but it does create some consistency issue in terms of spacing (as you might have noticed on the page).
impressive topic
Hi Deri. Yes it is!