
For the very vast majority of humans on earth, there is a topic found in the good old math textbooks that many of us still even dread contemplating about, as it seems to mess with our brain in a rather particular way. The name? Logarithmus — or Logarithm in English to be sure!
As terrible-sounding as it is, logarithm seems to have this distinct characteristic of metaphorically leaving a bad taste in our mouth. In fact, even for those who managed to maneuver around it back in high school, logarithm still remains largely as an evasive concept. The “I-can-manipulate-expressions-without-understanding-anything” syndrome runs rampant when it comes to logarithm.
Indeed, here in North America, the grade school curriculum has the propensity of overemphasizing the mechanics at the expense of basic theory, leaving us with the formidable task of filling in the logarithmic knowledge gap, which includes — among others — the theory behind the properties of logarithm, and its intended computational use in handling numbers with an order of magnitude veering towards the extremes.
So with that in mind, if you think that the time might have finally come to tame this monster we call logarithm, then it would be our pleasure to congratulate your timing on this very honorable act. And if you are simply looking to explore further into the rabbit hole, that would be doubly appreciated as well, for regardless of your motivation, the taming/musing is on! 🙂
Table of Contents
Logarithm — A Review
Terminology
Given a real number $x$, one of the challenges in elementary algebra is to express $x$ as a power of another number $b$ (known as the base). More specifically, we are interested in finding a number $\Box$ such that:
\begin{equation*} x = b^\Box \end{equation*}
As it turns out, this problem — in the crude form that it currently is at least — needs to be patched up first before any meaningful discussion can take place. For example:
- If the base is negative, then its powers need not be necessarily well-defined (e.g., $\displaystyle (-e)^{\frac{1}{2}}$).
- If the base is $\displaystyle 1$, then any power of it would be just $1$, in which case, it would be impossible for it to generate any number that’s not $1$. A similar remark applies to the case where the base is equal to $0$.
For these reasons, in the context of power determination, it’s customary to require the base $b$ to be a positive number — that is not equal to $1$. While under this assumption, any power of $b$ would necessarily have to be positive, it would also transpire —under this setup — that any positive number can be expressed as a power of $b$ in a unique way. That is, as long as $x$ is positive, there will be a unique number $\Box$ (known as the exponent) such that:
\begin{equation*} x= b^{\Box} \end{equation*}
in which case, we will simply call $\Box$ the logarithm of $x$ (in base $b$). In other words, logarithm is basically what happens when we expressed a number as a power, and then take the exponent from that power — It gives us the magnitude of a number, with respect to the base in question.
For example, when we try to express the number $64$ as a power of $2$, we get that $64= 2^6$. This alone shows that $6$ is the logarithm of $64$ — with respect to the base $2$.
Notation-wise, the logarithm of $x$ in base $b$ is denoted by $\log_b x$, with $x$ also being called the argument of the logarithm. When considered as a function, $\log_b x$ is defined on all positive numbers — as long as the base $b$ is valid (i.e., $\displaystyle b>0, b \ne 1$) .
To begin, we first note that regardless of the value of the base $b$, we always have that:
- $\displaystyle \log_b 1 = 0$ (since $0$ is the number $b$ needs to be raised to yield $1$)
- $\displaystyle \log_b b = 1$ (since $1$ is the number $b$ needs to be raised to yield $b$)
- $\displaystyle \log_b \frac{1}{b} = -1$ (since $-1$ is the number $b$ needs to be raised to yield $\displaystyle \frac{1}{b}$)
Because these results are almost immediate and sufficiently notable, we’ll simply refer to them as the trivial logarithmic identities.
In addition, since $\log_b x$ stands for the number which exponentiates to $x$, we also have that by definition:
\begin{align*}b^{\log_b x} & = x \qquad (\text{for all }x>0)\end{align*}
On the other hand, we also have that:
\begin{align*} \log_b (b^x) = x \qquad (\text{for all } x \in \mathbb{R}) \end{align*}
Since one can see by inspection that $x$ is precisely the number which exponentiates to $b^x$.
For example, since $\displaystyle \log_2 53$ is the number that $2$ needs to raise to yield $53$, we have that $\displaystyle 2^{\log_2 53} =53$. Similarly, since $\displaystyle 10^{-\pi}$ is a power of $10$ with the exponent $-\pi$, we can infer that $\displaystyle \log_{10} \left(10^{-\pi}\right) = -\pi$.
Common Logarithm (Base 10)
Being the inverse of the exponential function $\displaystyle 10^x$, the base-$10$ logarithmic function — also known as the common logarithm — is customarily denoted by $\log_{10} x$, $\log x$, or simply $\lg x$ for short. The common logarithm is of great interest to us, primarily due to the prevalence of the decimal number system in various cultures around the world.
Caution
Note that in older scientific texts and some textbooks in higher mathematics, $\log x$ can also refer to — and usually is — the natural logarithm of base $e$.
When the common logarithm of a number is calculated, the decimal representation of the logarithm is usually split into two parts: the integer component (a.k.a., characteristic) and the fractional component (a.k.a., mantissa). The characteristic in essence tells us the number of digits the original number has, and the mantissa hints at the extent to which this number is close to its next power of $10$. These are the facts that make common logarithm a particularly handy tool in determining the order of magnitude of an exceptionally large (or small) number.
For example, to figure out the magnitude of the number $50!$ (i.e., $50 \times \cdots \times 1$), we proceed to calculate its logarithm, yielding that: \[ \log (50!) \approx 64.483 \] which means that $50! \approx 10^{64.483} =$ $10^{64}10^{0.483} \approx$ $10^{64} \cdot 3.04$, suggesting that $50!$ is a $65$-digit number which starts with $3$ — the characteristic $64$ gives away the number of digits, and the mantissa $0.483$ reveals the rest about the number itself.
Take home message? There is no need to write out a number in full to figure out its approximate size!
Binary Logarithm (Base 2)
Being the inverse of the exponential function $2^x$, the binary logarithm function $\log_2 x$ is extensively used in the field of computer science, primarily due to the fact that computers store information in bits (i.e., digits which takes $0$ or $1$ as possible values).
Similar to the case in base $10$, binary logarithm can be used to figure out the number of digits of a positive integer in binary representation. In addition, binary logarithm is also used to figure out the depth of a binary tree, or even the number of operations required by certain computer algorithms (this falls into a topic known as algorithmic time complexity).
Beyond the world of computers, binary logarithm is also used in music theory to conceptualize the highness of musical notes, based on the fundamental observation that raising a note by an octave increases the frequency of the note by twofold. As a result, it is often convenient to conceive a musical interval as the binary logarithm of the frequency ratio.
Natural Logarithm (Base $e$)
In some textbooks concerned with a more rigorous development of transcendental functions, the base-$\displaystyle e$ logarithmic function — otherwise known as natural logarithm, $\log_e x$ or simply $\ln x$ — are sometimes defined as the area between the reciprocal function $\frac{1}{x}$ and the x-axis from $1$ to $x$ (hence the term natural).
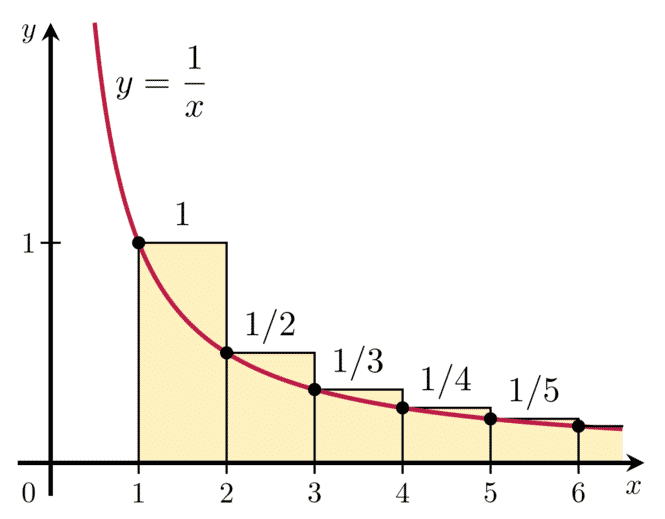
Under this definition, it could be shown that the inverse of $\ln x$ is precisely the natural exponential function $e^x$, leading to the following standard definition of natural logarithm:
Given a positive number $x$, $\ln x$ denotes the number $e$ needs to be raised — in order to become $x$.
Unlike the number $10$ — which is preferred due to the prevalence of decimal numbering system — the number $\displaystyle e$ is one of the special constants that pops up surprisingly often in various mathematical discourses — irrespective of the number system being chosen. As a result, mathematicians tend to consider base $e$ as more natural than base $10$ — even though some applied scientists and engineers beg to differ in various occasions…
Actually, to illustrate the scope of these intellectual biases among the scientific community, here’s an interesting account from Wikipedia on the historical development of the notations for logarithms:
Because base 10 logarithms were most useful for computations, engineers generally simply wrote “log(x)” when they meant log10(x). Mathematicians, on the other hand, wrote “log(x)” when they meant loge(x) for the natural logarithm. Today, both notations are found.
Since hand-held electronic calculators are designed by engineers rather than mathematicians, it became customary that they follow engineers’ notation. So the notation, according to which one writes “ln(x)” when the natural logarithm is intended, may have been further popularized by the very invention that made the use of “common logarithms” far less common, electronic calculators.
Logarithm of an Arbitrary Base
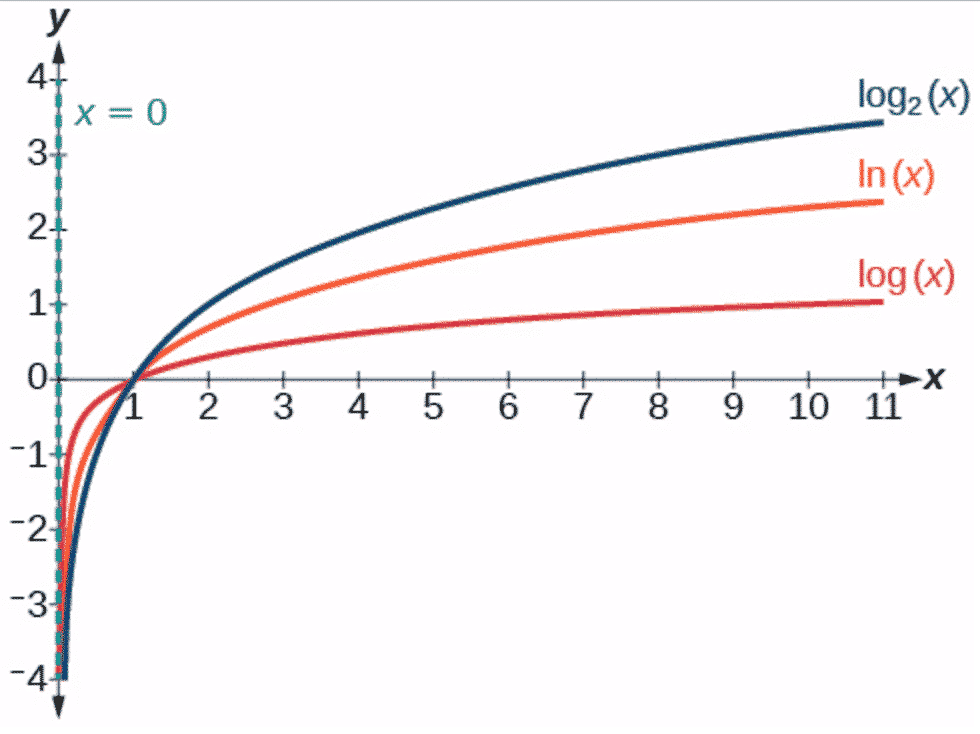
In addition to the three most popular logarithmic functions introduced earlier, one can also define logarithm using other valid bases as well. In practice, logarithm is generally employed with the intention of condensing large numbers (i.e., greater than $1$) into smaller numbers, so that the larger the base, the smaller the logarithm.
However, that’s only part of the story, as all the logarithmic functions we have encountered so far have bases exceeding the number $1$ (i.e., large base). In fact, in the cases where the base is strictly between $0$ and $1$ (i.e., small base), the graph of the logarithmic function will be turned upside down. Indeed, as opposed to a standard logarithmic function which increases from $-\infty$ to $\infty$, a small-base logarithmic function actually decreases from $+\infty$ to $-\infty$ as the argument increases.
Fortunately though, we rarely have to resort to this kind of logarithmic function in practice. As we shall see later with the Change of Base Rule, every pair of logarithmic functions are all but a multiple apart, so that in terms of applications and equation/inequality solving, the three standard logarithms are.generally more than enough to get things going.
Logarithmic Scale and its Applications
Since logarithm allows for mapping an exponential scale into a linear scale, it became an vital concept when it comes to communicating about a numerical variable whose quantities either grow exponentially, or shrink exponentially. Why? Because if we just take the logarithm of that variable, we are in effect turning that variable into something people refer to as a logarithmic scale.
While seemingly a highly-theoretical concept, logarithmic scale — when adopted appropriately — can be used to help us better explain/understand a surprising amount of phenomena found in nature. ranging from stuffs such as the loudness of a sound, the magnitude of an earthquake to the acidity of a solution and the highness of a musical pitch:
- In an equal-tempered piano, each key in the piano can be conceived as the binary logarithm of its relative sound frequency, so that every time we press a higher key on the piano, we are in effect increasing the sound frequency by a fixed factor ($\displaystyle \sqrt[12]{2}$ to be precise).
- In chemistry, the acidity of a solution is measured in pH, which is defined as the negative logarithm of the concentration of hydrogen ions. This basically means that as pH increases by $1$, the concentration of hydrogen ions decreases tenfold, leading to a substantially less acidic solution in return.
- In seismology, the severity of an earthquake can be quantified using the Richter scale, which is essentially the logarithm of the amplitude of seismic waves (relative to a threshold amplitude), so that every time the number on Richter scale increases by $1$, severity of the earthquake increases tenfold.
- In acoustics, the loudness of a sound is generally quantified using decibel (dB), which is a tenth of a bel (B), the latter of which is the logarithm of the sound power (relative to the threshold of hearing). In practice, this means that every increase of 10 dB (equiv., 1B), increases the sound power of a source by tenfold.
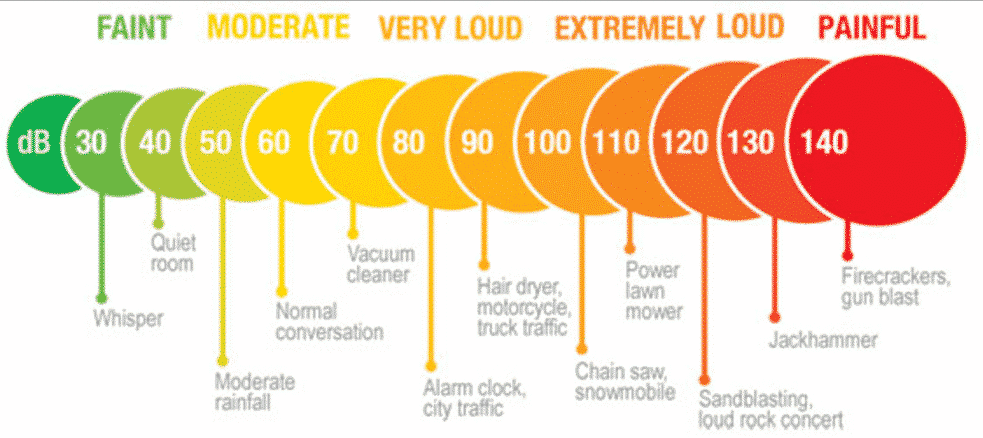
While not all logarithmic scales share the same base, the fact that one can hijack a concept such as logarithm — originally a purely-computational device — into an unifying abstract framework stringing together various seemingly unrelated phenomena found in nature, illustrates the power of the human mind and by extension, the thin line between mathematical invention and discovery.
Properties of Logarithm
Properties Involving the Arguments
One of the reasons why logarithm was such a powerful computational tool back in the old days — before the invention of computers or calculators — lies in the fact that one can always leverage certain properties of logarithm to reduce a complicated argument to its individual constituents — and doing so irrespective of the base in question. In what follows, we lay out five of such properties, which pertains to the product, the reciprocal, the quotient, the power and the root of a logarithm, respectively.
Product Rule
Given a product $xy$ and a base $b$, can we find the logarithm of $xy$ in terms of the logarithms of $x$ and $y$? As it turns out, the answer is a resounding yes, and a bit of inspection shows that $\log x + \log y$ is the number we are looking for. How so? Because that’s the number $b$ needs to be raised to get to $xy$:
\begin{align*} b^{\log x + \log y}= b^{\log x} \cdot b^{\log y} = xy \end{align*}
This fact — that logarithm of a product can be reduced into sum of logarithms of its constituents — gives rise to a property commonly known as the Product Rule.
Rule 1 — Product Rule for Logarithm
Given any two positive numbers $x$, $y$, we have that:
\begin{align*} \log (xy) =\log x + \log y \end{align*}
where all logarithms are assumed to be under the same valid base $b$.
In particular, when the base is $10$, the Product Rule can be translated into the following statement:
The magnitude of a product, is equal to the sum of its individual magnitudes.
For example, to gauge the approximate size of numbers like $365435 \cdot 43223$, we could take the common logarithm, and then apply the Product Rule, yielding that:
\begin{align*} \log (365435 \cdot 43223) & = \log 365435 + \log 43223 \\ & \approx 5.56 + 4.63 \\ & = 10.19 \end{align*}
which shows that $\displaystyle 365435 \cdot 43223$ is a 11-digit number close to $\displaystyle 10^{10.19} \approx 1.55 (10^{10})$.
Caution
Only apply the Product Rule when the preconditions are met. For example, one thing we cannot do is to break down $9$ into $-1$ and $-9$, and claim that $\ln 9 = \ln(-1) + \ln (-9)$.
And because an equality is by default bidirectional, instead of breaking the product by using the Product Rule from the left to the right, we can also use it from the right to the left, thereby turning a sum of logarithms into a product instead. For example:
\begin{align*} \log 25 + \log 4 = \log (25 \cdot 4) = \log 100 = 2 \end{align*}
On the downside however, since logarithm by default takes only positive numbers as arguments, applying logarithm and its properties to a function or an equation can significantly restrict its domain of feasibility. For example, while the function $x^2$ is defined on all real numbers, once we take the logarithm and apply the Product Rule, the resulting equality is still applicable — but now to the positive numbers only:
\begin{align*} \log (x^2) = \log x + \log x = 2 \log x\end{align*}
which serves as a good reminder that any logarithm-based algebraic technique — be it logarithmic equation solving, logarithmic inequality solving or logarithmic differentiation — should be carried out with this potential restriction in mind.
Reciprocal Rule
We know that every positive number has a multiplicative inverse (i.e., reciprocal), so perhaps there is also a shortcut in finding the logarithm of a reciprocal? Here again, the answer is a resounding yes. To see why, suppose that we are are given a positive number $x$, then by Product Rule, we have that:
\begin{align*} \log \left(x \ \cdot \frac{1}{x} \right) & = \log x + \log \left( \frac{1}{x} \right) \end{align*}
On the other hand, we also have that:
\begin{align*} \log \left(x \cdot \frac{1}{x} \right) & = \log 1 = 0 \end{align*}
Bridging the two equations together, we get that:
\begin{align*} \log x + \log \left( \frac{1}{x} \right) & = 0 \end{align*}
Or equivalently,
\begin{align*} \log \left( \frac{1}{x} \right) & = – \log x \end{align*}
Surprise! We just discovered the Reciprocal Rule, which states that to find the logarithm of a reciprocal, we just have to negate the logarithm of the original number.
Rule 2 — Reciprocal Rule for Logarithm
Given any positive number $x$, we have that:
\begin{align*} \log \left(\frac{1}{x} \right) = -\log x \end{align*}
where all logarithms are assumed to be under the same valid base $b$.
So instead of calculating the binary logarithm of $\displaystyle \frac{1}{512}$ from scratch, we could turn its head around and do:
\begin{align*} \log_2 \left( \frac{1}{512} \right) = -\log_2 512 = -9 \end{align*}
Quotient Rule
Now that both Product Rule and Reciprocal Rule are in order, let’s see what happens if we apply them to a quotient of positive numbers $x$ and $y$:
\begin{align*} \log \left( \frac{x}{y} \right) & = \log \left( x \cdot \frac{1}{y} \right) \\ & = \log x + \log \left( \frac{1}{y} \right) \\ & = \log x-\log y \end{align*}
Bingo! We have just shown that the logarithm of a quotient is precisely the difference between the original logarithms — a property commonly known as the Quotient Rule.
Rule 3 — Quotient Rule for Logarithm
Given any two positive numbers $x$ and $y$, we have that:
\begin{align*} \log \left( \frac{x}{y} \right) =\log x-\log y \end{align*}
where all logarithms are assumed to be under the same valid base $b$.
For example, instead to computing the natural logarithm of $\displaystyle \frac{2}{e}$ from scratch, we could apply the Quotient Rule, and get that:
\begin{align*} \ln \left( \frac{2}{e}\right) = \ln 2-\ln e = \ln 2-1 \end{align*}
As in the case with Power Rule, instead of breaking the quotient, we can also use the Quotient Rule from the right to the left, thereby turning a difference into a quotient instead. For example:
\begin{align*} \log 45-\log 9 = \log \left( \frac{45}{9} \right) = \log 5 \end{align*}
In base $10$, the Quotient Rule can also be translated into the following insight:
The magnitude of a quotient, is equal to the difference of the individual magnitudes.
which explains why in natural science, a quantity is often expressed in logarithmic scale, by taking the logarithm of the ratio between the said quantity and a reference point.
Power Rule
As for the logarithm of a number raised to an integer power, we begin by noting the case where a number is raised to $0$:
\begin{align*} \log (x^0) = \log 1 = 0 = 0 \log x \end{align*}
In the case where a number is raised to a positive integer $n$, the logarithm can be obtained through the repeated applications of Product Rule:
\begin{align*} \log (x^n) & = \log \underbrace{ \left(x \cdots x \right)}_{n \text{ times}} \\ & = \underbrace{\log x + \, \dots + \log x}_{n \text{ times}} \\ & = n \log x \end{align*}
And in the case where a number is raised to a negative integer of the form $-n$, a mix of Product Rule and Reciprocal Rule will do:
\begin{align*} \log (x^{-n}) & = \log \left[ \left( \frac{1}{x}\right)^n \right] \\ & = n \log \left( \frac{1}{x}\right) \\ & = -n \log x \end{align*}
Either way, we’ve just shown that when a number is raised to a integer power, the resulting logarithm is rescaled precisely by that power as well. This interesting finding would result in a key property of logarithm known as the Power Rule.
Rule 4 — Power Rule for Logarithm
Given any positive number $x$ and integer $n$, we have that:
\begin{align*} \log (x^n) = n \log x \end{align*}
where all logarithms are assumed to be under the same valid base $b$.
As some might have expected, the Power Rule is by itself a very powerful property. For one, it allows us to pull out the exponent from the argument of a logarithm, thereby normalizing a potentially gigantic / minuscule number (e.g., $\displaystyle \log_2 (3^{15}) = 15 \log_2 3$), Conversely, the Power Rule can also be used to push an exponent inside the argument of a logarithm, thereby producing a potentially-simpler expression (e.g., $\displaystyle 3 \ln 5 = \ln (5^3) = \ln 125$).
Caution
Make sure that the precondition is met before applying the Power Rule. For example, while $\ln (x^8)$ is defined on all non-zero numbers, the equation $\ln (x^8)=8 \ln x$ is only true when $x>0$. In this case though, the issue can be resolved by absolutizing $x$, yielding the equality $\ln (|x|^8) = 8 \ln |x|$ instead.
Similar to the case with Product Rule and Quotient Rule, Power Rule can be interpreted as follows in base $10$:
Root Rule
To find some shortcut in evaluating the logarithm of a root, we begin by observing that for all positive integer $n$, an application of Power Rule shows that:
\begin{align*} \log \left[ (\sqrt[n]{x})^n \right] = n \log (\sqrt[n]{x}) \end{align*}
On the other hand, we also have that:
\begin{align*} \log \left[ (\sqrt[n]{x})^n \right] = \log x \end{align*}
Bridging the two equalities together, we get that:
\begin{align*} n \log (\sqrt[n]{x}) = \log x \end{align*}
Or equivalently,
\begin{align*} \log (\sqrt[n]{x}) = \frac{\log x}{n} \end{align*}
Awesome! This shows that to figure out the logarithm of a $n$th root, all we have to do is to divide the logarithm of the original number by $n$ — An insight which results in another property of logarithm known as the Root Rule:
Rule 5 — Root Rule for Logarithm
Given any positive number $x$ and positive integer $n$, we have that:
\begin{align*} \log (\sqrt[n]{x}) = \frac{\log x}{n} \end{align*}
where all logarithms are assumed to be under the same valid base $b$.
Much like the Power Rule, the Root Rule is not only useful for its ability to pull out the root from the logarithm (as in $\displaystyle \log (\sqrt[12]{6}) = \frac{\log 6}{12}$), but for its ability to create a root out of nothing as well (as in $\displaystyle \frac{\ln 2}{5}=\ln (\sqrt[5]{2})$).
In base $10$, the Root Rule can be interpreted as follows:
When a number is rooted, the resulting magnitude is rescaled precisely by the degree of the root in question.
And when we combine Power Rule and Root Rule together, we get that for any rational number of the form $\displaystyle \frac{m}{n}$ ($m \in \mathbb{Z}, n \in \mathbb{N}$):
\begin{align*} \log x^{\frac{m}{n}} & = \log \left[ (\sqrt[n]{x})^m \right] \\ & = m \log (\sqrt[n] x) \\ & = \frac{m}{n} \log x \end{align*}
In fact, this is nothing more than a special instance of the Generalized Power Rule:
\begin{align*} \log (x^p) = p \log x \qquad (\text{for all }p \in \mathbb{R}) \end{align*}
which can be proved by showing that $p \log x$ is indeed the exponent to which the base $b$ needs to be raised — to produce $x^p$:
\begin{align*} b^{p \log x} & = \left( b^{\log x }\right)^p = x^p\end{align*}
And finally, here is an example illustrating all the argument-related properties of logarithm we have seen thus far:
\begin{align*} \log \left( \frac{5^3 \cdot \sqrt[4]{15}} {10^{66} \cdot e^{\pi}} \right) & = \log \left( 5^3 \cdot \sqrt[4]{15} \right) – \log \left( 10^{66} \cdot e^{\pi} \right) \\ & = \left [\log 5^3 + \log \sqrt[4]{15} \right] – \left[ \log (10^{66}) + \log (e^{\pi})\right] \\ & = 3 \log 5 + \frac{\log 15}{4} – 66 \log 10 – \pi \log e \end{align*}
Properties Involving the Bases
OK. So that was a bit of properties involving the argument of logarithm, but what if we want to tweak with the base instead? Well, we’ve got you covered on that one too! In what follows, we present four properties of logarithm involving the bases for your own pleasure. These are the Chain Rule, the Change-of-Base Rule, the Base-Swapping Rule and the Base-Argument Interchangeability.
Chain Rule
Suppose for a moment that you have mastered all the five properties of logarithm used to reduce a argument into its simplest constituents, but for one reason or another find the base rather annoying. What would you do?
In our case, we would to find an alternate formula for calculating the same logarithm — without having to resort to this base directly.
Actually, let’s begin by tightening the question a bit: given a positive number $x$, is there a way of calculating $\log x$ (under base $b$) using a new base $a$? Or even better: what’s an expression involving $a$, such that when $b$ raised to it, becomes $x$?
Here, to find one such expression, it would be just natural to start with $\displaystyle \log_a x$ and see where it takes us from there. By definition, $\displaystyle \log_a x$ is just the number that $a$ needs to be raised, to become $x$. That is:
\begin{align*} a^{\log_a x} = x \end{align*}
But herein lies a problem: we want the left hand side to be a power of $b$ though. How can we turn that $a$ into $b$? Well, if we write $a$ as a power of $b$ that is! With this newfound insight, we proceed to replace the bottom $a$ with $\displaystyle b^{\log a}$, yielding that:
\begin{align*} {\left( b^{\log a} \right)}^{\log_a x} = b^{\log a \cdot \log_a x} = x \end{align*}
Bingo! The exponent in the middle term is exactly what we were looking for — the expression that $b$ needs to be raised, to become $x$! We can therefore conclude that:
\begin{align*} \log x = \log a \cdot \log_a x \end{align*}
In English, this reads:
The logarithm of a number, can be evaluated as the logarithm of a new base, times the logarithm of the original number under that new base.
In fact, this property is so impressive, that we decided to baptize it as the Chain Rule (not to be confused with the usual chain rule in calculus).
Rule 6 — Chain Rule for Logarithm
Given any positive number $x$ and valid base $a$, we have that:
\begin{align*} \log x = \log a \cdot \log_a x \end{align*}
where all the logarithms whose base isn’t explicitly defined are assumed to be under the same valid base $b$.
Here, an example illustrating its use is definitely called for: suppose that we’re given the task of determining the magnitude of the number $1024$ (i.e., find $\log_{10} 1024$), but figure that it would easier if the base were in $2$ instead, then one thing that we can do would be to apply the Chain Rule with $2$ as the new base, yielding that:
\begin{align*} \log_{10} 1024 = \log_{10} 2 \cdot \log_2 1024 = \log_{10} 2 \cdot 10 \approx 3.01 \end{align*}
so the magnitude of $1024$ is approximately $3.01$ (i.e., $1024 = 10^{3.01}$), which is consistent with it being a 4-digit number.
In fact, here is more: it actually doesn’t matter which new base we choose to use! The base could have been $3$, $e$ or even $\pi$, and the result would have been exactly the same!
\begin{align*} \log_{10} 1024 & = \log_{10} 3 \cdot \log_3 1024 \\ & = \log_{10} e \cdot \log_e 1024 \\ & = \log_{10} \pi \cdot \log_{\pi} 1024 \end{align*}
Change-of-Base Rule
If you’re still hanging around, you remember that Chain Rule states that:
\begin{align*} \log x = \log a \cdot \log_a x \end{align*}
Here, if we just solve for $\log_a x$, we would get:
\begin{align*} \log_a x = \frac{\log x}{\log a} \end{align*}
Goodness! Another alternate formula for logarithm! Except that this time, it’s an (in)famous one for real. The name? Change-of-Base Rule!
Rule 7— Change-of-Base Rule for Logarithm
Given any positive number $x$ and valid base $a$, we have that:
\begin{align*} \log_a x = \frac{\log x}{\log a} \end{align*}
where the logarithms whose base isn’t explicitly defined are assumed to be under the same valid base $b$
At the first sight, this might seem like a mere reformulation of the Chain Rule. However, upon further inspection, one can see that this is actually not the case: what the Chain Rule does is to turn a logarithm into a product of logarithms with different bases, while the Change-of-Base Rule turns a logarithm into a quotient of logarithms with the same base. In addition, the Chain Rule marginally facilitates the evaluation of a logarithm under a new base, while the Change-of-Base Rule actually fully eliminates the dependence on the old base.
In practice, the Change-of-Base Rule is primarily used to compute a “non-standard” logarithm by turning it into a quotient of “standard logarithms” (e.g., $\log_{15} 26 = \frac{\ln 26}{\ln 15} = \frac{\log_2 26}{\log_2 15}$). However, it can also be used in the reverse manner, thereby merging a quotient of logarithms into a single logarithm (e.g., $\frac{\ln 8}{\ln 2} = \log_2 8 = 3$).
In fact, both the Chain Rule and the Change-of-Base Rule provide a unifying framework for logarithms of all valid bases, by showing that every logarithmic function is a multiple apart from one another. With the advent of computers and calculators, the Change-of-Base Rule also opens up the practice of calculating a logarithm of an arbitrary base, by standardising it to base $e$, or — if a scientific calculator is used — to base $10$.
Base-Swapping Rule
Now, let’s do something fun. Remember that the Change-of-Base Rule states that:
\begin{align*}\log_a x = \frac{\log x}{\log a} \end{align*}
with the understanding that the “baseless” logarithms are actually assumed to be under some valid base $b$. Out of curiosity, if we just let this base to be $a$, we get that:
\begin{align*}\log_a x = \frac{\log_a x}{\log_a a} = \log_a x \end{align*}
which is not terribly interesting, as we are basically going in full circle. However, in the very special case where $x \ne 1$, we can let $x$ to be the base instead, thereby producing the following identity:
\begin{align*}\log_a x = \frac{\log_x x}{\log_x a} = \frac{1}{\log_x a}\end{align*}
Impressive! It’s almost like playing LEGO®! And since no one has given it a name yet, let’s just jump in and baptize it as the Base-Swapping Rule.
Rule 8 — Base-Swapping Rule for Logarithm
Given any two valid bases $x$ and $a$, we have that:
\begin{align*}\log_a x = \frac{1}{\log_x a}\end{align*}
In English, the Base-Swapping Rule translates into the following insight:
An alternate way of figuring out the logarithm of a number under a base, is to find the logarithm of the base under that number instead, and then take the reciprocal.
Terrible pun we know, but if you really hate operating under a certain base, the Base-Swapping Rule provides a quick-and-dirty way to get rid of it. For example:
\begin{align*} \log_{512} 2 = \frac{1}{\log_2 512} = \frac{1}{9}\end{align*}
which shows that mental LEGO can be just as fun as playing with a few dozen pieces of colored plastic. 🙂
Base-Argument Interchangeability
As a general rule of thumb, we don’t want to mess around with the bases and arguments by swapping them around. However, in the very special case where a base is raised to a logarithm, a bit of swapping actually preserves the equality, and is sometimes even preferred — like this:
\begin{align*} x^{\log y} & = y^{\log x} \end{align*}
In case you’re wondering about the exact nature of this black magic, here’s a proof showing how the left-hand side becomes the right-hand side:
(Note: all logarithms are assumed to be under base $b$)
\begin{align*} x^{\log y} & = {\left( b^{\log x} \right)}^{\log y} \\ & = {\left( b^{\log y} \right)}^{\log x} \\ & = y^{\log x} \end{align*}
Impressive property! For the lack of better term, let’s just refer to it as the Base-Argument Interchangeability!
Rule 9 — Base-Argument Interchangeability for Exponent
Given any two positive numbers $x$ and $y$, we have that:
\begin{align*} x^{\log y} & = y^{\log x} \end{align*}
where all logarithms are assumed to be under the same valid base $b$.
To illustrate the mechanics of this amazing property, here’s a fancy example for your pleasure:
\begin{align*} {\left( 2^{\ln 3} \right)}^{\ln 4} & = {\left( 3^{\ln 2} \right) }^{\ln 4} & (\text{swapping }2 \text{ and }3)\\ & = 4^{\ln \left( 3^{\ln 2} \right) } & (\text{swapping } 3^{\ln 2} \text{ and } 4)\\ & = 4^{\ln \left( 2^{\ln 3} \right) } & (\text{swapping }3 \text{ and }2)\\ & = {\left( 2^{\ln 3} \right)}^{\ln 4} & (\text{swapping }4 \text{ and }2^{\ln 3})\end{align*}
Kind of fun, right? Great place to pull the curtain on the properties of logarithm too! 🙂
Logarithm for Complex Numbers (Optional)
As you might have heard people saying on multiple occasions, logarithm — for most practical purposes at least — is defined only on the positive real numbers. Why? Because a number can only have logarithm if it’s expressible as a power, which in turn must be positive — by virtue of the definition of real-valued exponential functions.
However, as one would expect, this doesn’t sit well with a certain group of mathematical freedom fighters, for whom the following question might be more relevant:
Is there anything we can do to expand the domain of logarithmic functions to other numbers as well?
The answer? Yes, but not without some string attached. As it turns out, forcing this domain expansion will inevitably incur some painful sacrifices on many fronts, which include — among others — a substantial loss in the properties of exponent and logarithm.
Redefining the Exponential Function (of Base $e$)
To begin, we do know that defining the natural exponential function solely on the real numbers is a major stumbling block which needs to go, for it is precisely what restricted the exponentials to the positive numbers in the first place. To extend the definition of the natural exponential function to any complex number, we begin by redefining the exponential function as follows:
\begin{align*} e^{x+yi} \, \stackrel{def}{=} \, e^x \cdot e^{yi} \qquad ( \text{for all }x, y \in \mathbb{R})\end{align*}
which is of course consistent with the original definition of $\displaystyle e^x$ on the real numbers, as it can be seen that for all $\displaystyle x \in \mathbb{R}$:
\begin{align*} e^{x} = e^{x+0i} = e^x \cdot e^{0i} = e^x \cdot e^0 = e^x \end{align*}
But then, how do we interpret this redefinition now that we are in the realm of complex numbers? For one, by Euler’s Formula, we know that $e^{yi}$ stands for the unit complex number with angle $y$. In addition, since multiplying a complex number by a real positive constant results in the rescaling of the number by that same constant, it becomes apparent that the natural exponential function — as defined above — maps a complex number $x+yi$ to another complex number whose length is $e^x$ and whose angle is $y$.
(In fact, this key redefinition of exponential would later play a central role in the development of complex analysis, and in ancillary fields such as Laplace transform as well.)
For example, $\displaystyle e^0=1, e^1=e, e^{\frac{\pi}{2}i}=i, e^{\pi i}=-1$ and $\displaystyle e^{1+ \pi i} =$ $\displaystyle e^1 \cdot e^{\pi i} = -e$. In fact, one can also see that by construction, any exponential is necessarily a number with non-zero length (i.e., an exponential is always non-zero).
Redefining the Logarithmic Function (of Base $e$)
So the natural exponential function maps the entire complex plane to non-zero complex numbers, but perhaps what is more subtle is the fact that any non-zero complex number can be expressed as a power of $e$ as well. To see why, suppose that we are given a non-zero complex number $\displaystyle z$, then as long as we let:
- $x$ be the number such that $e^x$ is equal to the length of $\displaystyle z$ (remember, this is always possible, since $z$ is a non-zero number, and hence must have non-zero length as well)
- $y$ be an angle of $\displaystyle z$
then we will have that:
\begin{align*} e^{x+yi} & = e^x \cdot e^{yi} \\ & = \text{the complex number with the length and angle of }z \\ & = z \end{align*}
More specifically, given any non-zero complex number $\displaystyle z$, if $\displaystyle |z|$ stands for the length of $\displaystyle z$ and $\theta$ an angle of $\displaystyle z$, then we have just shown that:
\begin{align*} e^{\ln |z|+\theta i} & = e^{\ln |z|} \cdot e^{\theta i} \\ & = \text{the complex number with the length and angle of } z \\ & = z \end{align*}
In other words, we have just found a logarithm of $z$ — $\displaystyle \ln |z|+\theta i$ that is! However, notice the use of “a” instead of “the“, for as alluded to a bit earlier, this is not going to go all smoothly…
For one, since a complex number can have several equivalent angles, defining the natural exponential function on the entire complex plane can open up a whole can of worms — That is, a whole can of infinitely-many complex numbers whose exponentials are all but the same. For example:
\begin{align*} e^{\pi i}= e^{3 \pi i} = e^{5 \pi i} = e^{- \pi i} = \dots = -1 \end{align*}
which shows that the logarithm of $-1$ — or any other number for that matter — is ill-defined with this current setup.
Naturally, one way to remedy this multivalue-ness of logarithm is to restrict the domain of the exponential function to the principal branch. That is, the set of complex numbers whose imaginary part lies in the interval $\displaystyle (-\pi, \pi]$. With the domain restricted this way, we will then be able to prove that the exponentials of distinct numbers are themselves distinct, making the natural exponential an invertible function — mapping the principal branch to the set of non-zero complex numbers.
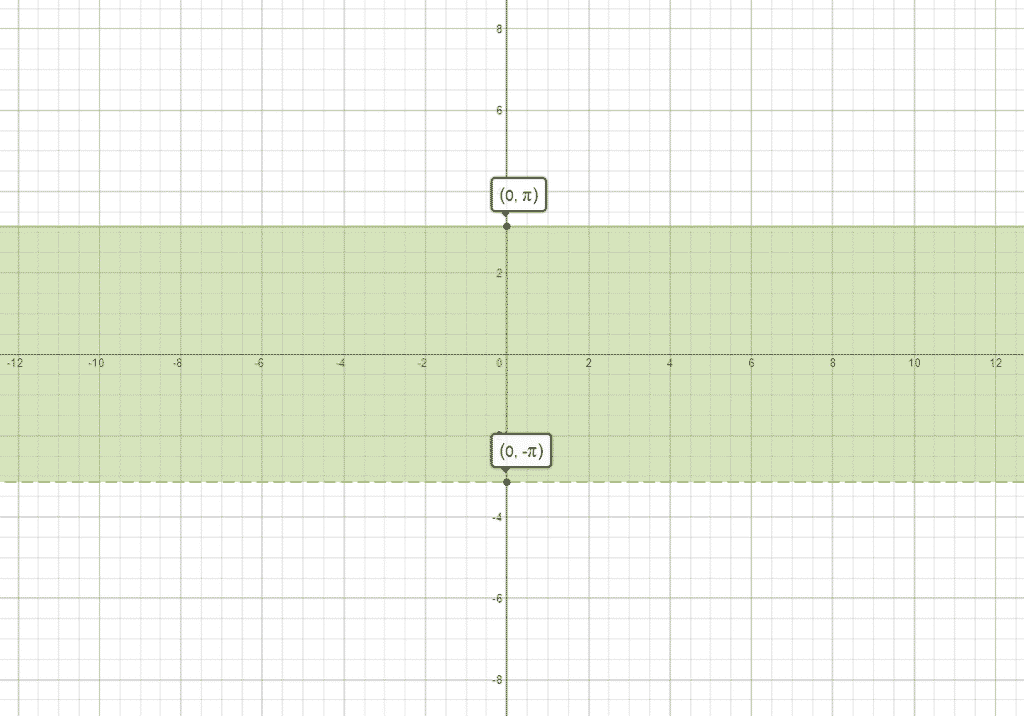
Under this setup, the inverse of the exponential function — the natural logarithmic function — maps the set of non-zero complex numbers to the principal branch. In fact, it can be shown that: \[ \boxed{ \ln z = \ln |z| + (\arg{z}) i \ } \]
where $\arg{z}$ stands for the principal angle of $\displaystyle z$ (i.e., the angle in the interval $\displaystyle (-\pi, \pi]$). For example:
\begin{align*} \ln (-1) = 0+\pi i \qquad \ln (-5) = \ln 5 + \pi i \qquad \ln (-1+i)= \ln (\sqrt{2}) + \frac{3\pi}{4}i \end{align*}
Redefining Exponential Functions (of Arbitrary Bases)
With the definition of natural logarithm now taken care of, we can proceed to define the exponential function of an arbitrary base $\displaystyle a$ — simply by standardizing it into base $\displaystyle e$:
\begin{align*} a^{z} = {\left(e^{\ln a}\right)}^{z} \, \stackrel{def}{=} \, e^{(\ln a)z} \end{align*}
Of course, in order for this definition to make sense, the base $\displaystyle a$ has to be non-zero. In addition, the base must not be $\displaystyle 1$ either, otherwise we will just end up with a constant function instead. Basically, this just means that the concept of valid base also has to be updated — from a positive real number that’s not $\displaystyle 1$, to a non-zero complex number that’s not $\displaystyle 1$. And that’s a great achievement if you think about it: the set of valid bases have just gone from the right side of a real number line, to almost the entire complex plane!
Properties of Logarithm — An Update
So all seems to be good. Or is it? Underneath the surface, the properties of logarithm are actually falling apart:
- Product Rule fails: $\displaystyle \ln (-1 \cdot -1) = \ln 1 =0$, but $\displaystyle \ln (-1) + \ln (-1) = 2 \pi i$.
- Reciprocal/Quotient Rule fails: $\displaystyle \ln \left( 1/(-1) \right) = \ln (-1) = \pi i$, but $\displaystyle \ln 1-\ln(-1) = 0-\pi i = -\pi i$.
- Power Rule fails: $\displaystyle \ln \left[ (-1)^2 \right] = \ln 1 = 0$, but $\displaystyle 2 \ln (-1) = 2 \pi i$.
- Root Rule fails: The Fundamental Theorem of Algebra implies that a number can now have up to $n$ $n$th complex roots, so the concept of unique $n$th root is no longer applicable.
On a brighter side, logarithmic functions of an arbitrary base can now be defined — in terms of $\displaystyle \ln z$ — for all non-zero complex number, using an instance of what’s previously known as the Change-of-Base Rule:
\begin{align*} \log_a x \, \stackrel{def}{=} \, \frac{\ln x}{\ln a} \qquad (x \ne 0, a \text{ being a valid base}) \end{align*}
In light of this, it’s therefore no surprise that the full-fledged Change-of-Base Rule actually hold for complex logarithms in general:
\begin{align*} \log_a x & = \frac{\ln x}{\ln a} \\ & = \frac{\frac{\ln x}{\ln b}}{\frac{\ln a}{\ln b}} \\ & = \frac{\log_b x}{\log_b a} \qquad (x \ne 0, a \text{ and } b\text{ being both valid bases})\end{align*}
In particular, in the case where $x$ is also a valid base, we get that:
\begin{align*} \log_a x = \frac{\log_x x}{\log_x a} = \frac{1}{\log_x a} \end{align*}
What’s the name again? Base-Swapping Rule of course!
In addition, if we just start from the Change-of-Base Rule and solve for $\displaystyle \log_b x$, we get that the Chain Rule is here to stay as well:
\begin{align*} \log_b x = \log_b a \cdot \log_a x \qquad (x \ne 0, a \text{ and } b\text{ being both valid bases}) \end{align*}
In fact, it turns out that even the Base-Argument Interchangeability carries on as well, but only because of a special instance of “Power Rule” that we’ve built in into our definition of general exponential function:
\begin{align*} x^{\log_b y} & = e^{\ln x \cdot \log_b y} \\ & = e^{\frac{\ln x \cdot \ln y}{\ln b}} \\ & = e^{\ln y \cdot \log_b x} \\& =y^{\log_b x} \qquad (x, y \ne 0, b \text{ being a valid base}) \end{align*}
So that even though all properties of logarithm involving the arguments are lost in the process, those involving the bases all managed to come out of this unscathed.
Properties of Exponent — An Update
What about the properties of exponents though? In two words: not good. 🙁
- Trivial Identities holds: $\displaystyle a^0= 1, a^1=a$.
- Additive Properties holds: For all $\displaystyle z_1, z_2 \in \mathbb{C}$, $\displaystyle a^{z_1+ z_2} = a^{z_1} a^{z_2}$ and $\displaystyle a^{z_1 – z_2} = \frac{a^{z_1}}{a^{z_2}}$.
- Common-Exponent Properties fails: Given $a,b \ne 0$, we have that $\displaystyle (ab)^x \ne a^x b^x$ and $\displaystyle \left(\frac{a}{b}\right)^x \ne \frac{a^x}{b^x}$ in general.
- Power Property fails: $\displaystyle \left( a^{z_1}\right)^{z_2} = a^{z_1 \cdot z_2}$ when the outer exponent $z_2$ is an integer (thanks to the Additive Properties of exponent!), but is otherwise false in general.
Basically, every property — whose validity depends on the argument-related properties of logarithm — will fall out big time.
And finally, to ease the information overload, here’s a summary of the overall gains and casualties associated with expanding the domains of exponential and logarithmic functions:
- As long as we restrict to the domain of $\displaystyle e^z$ to a branch, we can define logarithm on all non-zero complex numbers — and doing so using any valid base under the sun.
- However, the five properties of logarithm involving the arguments (e.g., Product Rule, Reciprocal Rule, Quotient Rule, Power Rule, Root Rule) will be lost in the process.
- Surprisingly though, the four properties of logarithm involving the bases (i.e., Change-of-Base Rule, Chain Rule, Base-Swapping Rule, Base-Argument Interchangeability) will be all preserved.
- Due to the substantial loss in the properties of logarithm, most of the properties of exponent will be falling apart as well.
So in retrospect, is it worth the effort going through the hurdle of expanding the domain of logarithmic functions? Heck, guess we’ll let you decide on that one! 🙂
Afterwords
Whew! Who would have thought that a pure venture into some basic theory can take us this far! Originally a tool for computing large numbers (e.g., turning products or quotients into sums or differences) and for solving exponential equations (through the properties of logarithm), logarithm has obviously gone a long way into finding itself in various branches of both applied sciences and pure mathematics.
For the applied scientists, logarithm tends to bring to mind topics such as order-of-magnitude computation (decimal or binary), logarithmic scales (e.g., frequency in musical notes, Richter scale, pH, sound loudness), algorithmic complexities and log-normal distribution. For others who live in the ivory tower (who’s that?), logarithm is often associated with idealized objects such as the harmonic series, reciprocal funcion, and even prime numbers,
In fact, when we toyed around the idea of incorporating complex numbers into logarithm, we found that not only were we able to extend the definition of logarithm to the negative real numbers, but to any other non-zero complex number as well. While the extension doesn’t always end up as the way we wanted, doing so actually paves the way of introducing complex logarithm into other seemingly-unrelated subjects, such as integration by partial fractions in calculus for instance.
And before someone’s brain blows up, here’s an interactive table for what we’ve found thus far:
| Base |
| Exponent |
| Power |
| (Order of) Magnitude |
| Exponentiation |
| Argument (of a Logarithm) |
| Definition of Logarithm: $\displaystyle b^{\log_b x} = x \quad (x>0)$ |
| Inverse Relationship Between Exponential and Logarithmic Function: $\displaystyle \log_b (b^x) = x$ |
| Trivial Logarithmic Identities: $\displaystyle \log_b 1 = 0$, $\displaystyle \log_b b = 1$, $\displaystyle \log_b \frac{1}{b} = -1$ |
Common Logarithm (Base 10)
| $\displaystyle \log x$ |
| Number of Digits (Decimal Representation) |
| Characteristic |
| Mantissa |
Binary Logarithm (Base 2)
| $\displaystyle \log_2 x$ |
| Number of Bits (Binary Representation) |
| Binary Tree |
| Number of Required Operations (Algorithm) |
| Octave (Music) |
| Frequency (Musical Notes) |
Natural Logarithm (Base e)
| $\displaystyle \ln x$ |
| Reciprocal Function |
| Natural Exponential Function |
| Harmonic Series |
| $\displaystyle \log x$ (Notational Ambiguity) |
Logarithm (Arbitrary Base)
| Valid Base |
| Large Base |
| Small Base |
| Graph (Logarithmic Functions) |
Terminology
| Linear Scale vs. Logarithmic Scale |
| Exponential Growth/Shrinking |
Applications
| Frequency of Musical Notes (Music Theory): Relative note frequencies converted into binary logarithm. Increase a semitone increases the frequency of a note by $\displaystyle \sqrt[12]{2}$. |
| pH (Chemistry): Concentration of hydrogen ions converted into negative (common) logarithm. Increase pH by $1$ decreases the acidity of a solution by tenfold. |
| Richter Scale (Seismology): Relative seismic wave amplitude converted into common logarithm. One unit of increase in Richter scale increases the severity of an earthquake by tenfold. |
| Decibel (Acoustics): Relative sound power converted into common logarithm (with the unit in bel), where one bel of increase boosts the relative sound power by tenfold. |
Assuming that all logarithms below are defined under a valid base $b$, then the following properties hold:
| Product Rule: $\displaystyle \log (xy) =\log x + \log y \quad (x,y >0)$ |
| Reciprocal Rule: $\displaystyle \log \left(\frac{1}{x} \right) = – \log x \quad (x>0)$ |
| Quotient Rule: $\displaystyle \log \left( \frac{x}{y} \right) =\log x – \log y \quad (x,y>0)$ |
| Power Rule: $\displaystyle \log (x^n) = n \log x \quad (x>0, n \in \mathbb{Z})$ |
| Root Rule: $\displaystyle \log (\sqrt[n]{x}) = \frac{\log x}{n} \quad (x>0, n \in \mathbb{N})$ |
| Generalized Power Rule: $\displaystyle \log (x^p) = p \log x \quad (x>0, p \in \mathbb{R})$ |
Given two valid bases $a, b$, and that all logarithms with no explicit base are defined under the base $b$, then the following properties hold:
| Chain Rule: $\displaystyle \log x = \log a \cdot \log_a x \quad (x>0)$ |
| Change-of-Base Rule: $\displaystyle \log_a x = \frac{\log x}{\log a} \quad (x>0)$ |
| Base-Swapping Rule: $\displaystyle \log_a x = \frac{1}{\log_x a} \quad (x \text{ being also a valid base})$ |
| Base-Argument Interchangeability: $\displaystyle x^{\log y} = y^{\log x} \quad (x,y >0)$ |
| Natural Exponential Function: $\displaystyle e^{x+yi} \, \stackrel{def}{=} \, e^x \cdot e^{yi} \quad ( \text{for all }x, y \in \mathbb{R})$ |
| Natural Logarithmic Function: For any non-zero complex number $\displaystyle z$, $\ln z \, \stackrel{def}{=} \, \ln |z| + (\arg{z}) i$, where $\displaystyle |z|$ stands for the length of $\displaystyle z$, and $\displaystyle \arg{z}$ the principal angle of $\displaystyle z$ in the interval $\displaystyle (-\pi, \pi]$. |
| Valid Base: Changes from a positive real number that is not equal to one, to any non-zero complex number that is not equal to one. |
| Exponential Function (Arbitrary Base): $\displaystyle a^{z} \, \stackrel{def}{=} \, e^{(\ln a)z} \quad (a \text{ being a valid base})$ |
| Logarithmic Function (Arbitrary Base): $\displaystyle \log_a x \, \stackrel{def}{=} \, \frac{\ln x}{\ln a} \qquad (x \ne 0, a \text{ being a valid base})$ |
| Properties of Logarithm: All rules involving the arguments fall apart (i.e., Product Rule, Reciprocal Rule, Quotient Rule, Power Rule and Root Rule). On the other hand, all rules involving the bases are preserved (i.e., Chain Rule, Change-of-Base Rule, Base-Swapping Rule, Base-Argument Interchangeability) |
| Properties of Exponents: Trivial Properties (i.e. $\displaystyle a^0=1, a^1=a$) and Additive Properties (i.e., $\displaystyle a^{z_1+ z_2} = a^{z_1} a^{z_2}, \, a^{z_1 – z_2} = \frac{a^{z_1}}{a^{z_2}}$) remain. All other properties which rely on the argument-related properties of logarithm fail (e.g., Common-Exponent Properties, Power Property). |
All right. Here’s a wrap for the fascinating topic known as the logarithm, so whether you prefer it real or complex, or you’d rather have it algebraic or applied, at least there’s now no more excuse to avoid them!


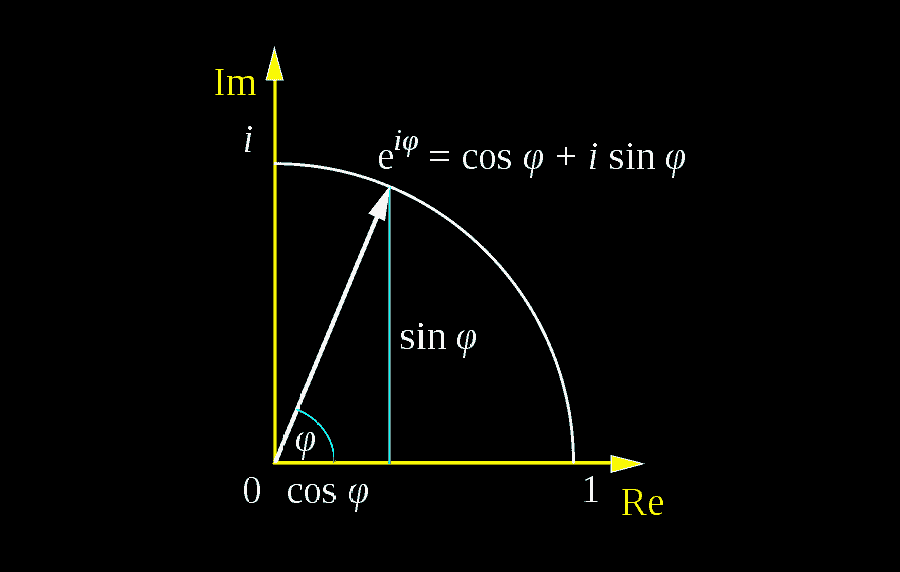
Great job guys! 😀
I enjoyed reading this, brushing up on my log skills in a surprisingly well written format.
Just a few things to point out,
I think you got the brackets wrong in the example after rule 9 — that really threw me off.
You misspelled precisely as percisely in the first paragraph of redefining the natural log in complex numbers
Once again, Bravo! 🙂
Hi Anitej! Glad you like it! Yep. no more “percisely” anymore — sometimes we’re so close to the materials that it’s hard for us to see it despite numerous proofreadings.
Also, we just threw in some justifications for the example underneath Rule 9, see if it helps. 🙂
Great then, thank you!
One of the things that makes this site so great is how quickly you guys reply and update your articles/guides. Rest assured you’ve found a regular visitor in me, and I will share this with everyone I deem fit — calling it my dirty secret to Math! 😉
Talks about the power of digital vs. traditional publishing. And dirty little secret sounds about just right! 🙂
Good& useful for Brush-up.
Thank you!
Unfortunately, your introduction to Logs has made my understanding even more confused.
Hi Edwin. This is a comprehensive guide to logarithm from a higher math perspective. For a more elementary guide, you might want to check out this logarithm article on MathIsFun for more.