Let us take a moment to ponder how truly bizarre the Laplace transform is.
You put in a sine and get an oddly simple, arbitrary-looking fraction. Why do we suddenly have squares?
You look at the table of common Laplace transforms to find a pattern and you see no rhyme, no reason, no obvious link between different functions and their different, very different, results.
What’s going on here?
Or so we thought when we first encountered the cursive $\mathcal{L}$ in school.
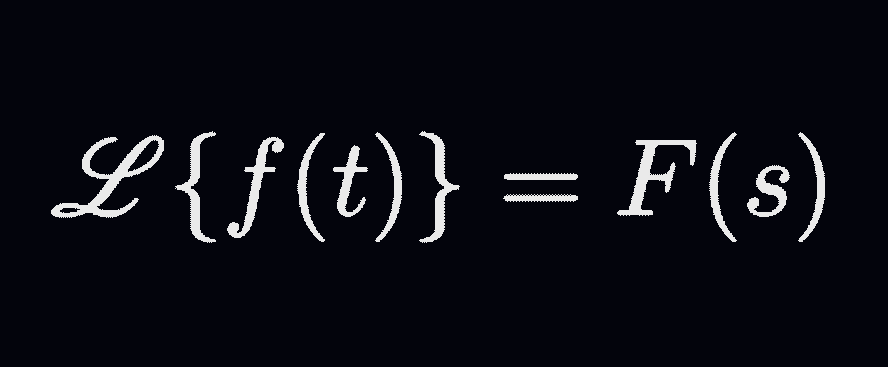
Table of Contents
What does the Laplace transform do, really?
At a high level, Laplace transform is an integral transform mostly encountered in differential equations — in electrical engineering for instance — where electric circuits are represented as differential equations.
In fact, it takes a time-domain function, where $t$ is the variable, and outputs a frequency-domain function, where $s$ is the variable. Definition-wise, Laplace transform takes a function of real variable $f(t)$ (defined for all $t \ge 0$) to a function of complex variable $F(s)$ as follows:
\[\mathcal{L}\{f(t)\} = \int_0^{\infty} f(t) e^{-st} \, dt = F(s) \]Some Preliminary Examples
What fate awaits simple functions as they enter the Laplace transform?
Take the simplest function: the constant function $f(t)=1$. In this case, putting $1$ in the transform yields $1/s$, which means that we went from a constant to a variable-dependent function.
(Odd but not too worrying. After all, we’ve seen $1/x$ integrating to $\ln x$ in calculus. Not a constant-to-variable situation of course, but an unexpected transformation nonetheless.)
Let us take it up a notch, with the linear function $f(t) = t$. After the transformation, it is turned into $1/s^2$, which means that we went from $1 \to 1/s$ to $t \to 1/s^2$. A pattern begins to emerge.
Now what about $f(t)=t^n$? With this simple power function, we end up with: \[ \mathcal{L}\{ t^n \} = \frac{n!}{s^{n+1}}\] So there was a factorial in $\mathcal{L}\{t\}$ all along, hidden by the fact that $1! = 1$. What else is the transform hiding?
Here, a glance at a table of common Laplace transforms would show that the emerging pattern cannot explain other functions easily. Things get weird, and the weirdness escalates quickly — which brings us back to the sine function.
Looking Inside the Laplace Transform of Sine
Let us unpack what happens to our sine function as we Laplace-transform it. We begin by noticing that a sine function can be expressed as a complex exponential — an indirect result of the celebrated Euler’s formula:\[e^{it} = \cos t + i \sin t\]In fact, a sine is often expressed in terms of exponentials for ease of calculation, so if we apply that to the function $f(t) = \sin (at)$, we would get: \[ \sin(at) = \frac{e^{iat}-e^{-iat}}{2i} \]Thus the Laplace transform of $\sin(at)$ then becomes:
\[ \mathcal{L}\{\sin(at)\} = \frac{1}{2i} \int\limits_0^{\infty} (e^{iat}-e^{-iat}) e^{-st} \, dt \]which means that we have a product of exponentials. Distributing the terms, we get:
\[ \mathcal{L}\{\sin(at)\} = \frac{1}{2i} \int\limits_0^{\infty} e^{iat-st}-e^{-iat-st} \, dt \]
Here, factoring the $t$ in the exponents yields:
\[ \mathcal{L}\{\sin(at)\} = \frac{1}{2i} \int\limits_0^{\infty} e^{(ia-s)t}-e^{(-ia-s)t} \, dt \]and since $\mathrm{Re}(s) \gt 0$ by assumption, we can proceed with the integration from $0$ to $\infty$ as usual:
\[ \mathcal{L}\{\sin(at)\} = \left.\frac{e^{(ia-s)t}}{2i (ia-s)}\right|_0^{\infty}-\left.\frac{e^{(-ia-s)t}}{2i (-ia-s)}\right|_0^{\infty} \]
Let us simplify further. Distributing the $i$ inside the parentheses, we get:
\[ \mathcal{L}\{\sin(at)\} = \left.\frac{e^{(ia-s)t}}{2(-a-is)}\right|_0^{\infty}-\left.\frac{e^{(-ia-s)t}}{2(a-is)}\right|_0^{\infty} \]By evaluating the $t$ at the boundaries, we get:
\[ \mathcal{L}\{\sin(at)\} = \left( \frac{e^{(ia-s) \cdot \infty}}{2(-a-is)}-\frac{e^{(ia-s) \cdot 0}}{2 (-a-is)}\right)-\left(\frac{e^{(-ia-s)\cdot\infty}}{2(a-is)}-\frac{e^{(-ia-s)\cdot 0}}{2(a-is)}\right) \]And because $\mathrm{Re}(s) > 0$ by assumption, both $e^{(ia-s) \cdot \infty}$ and $e^{(-ia-s)\cdot\infty}$ oscillate to $0$ (i.e., vanish at infinity), after which we are then left with:\[ \mathcal{L}\{\sin(at)\} = \frac{1}{-2(-a-is)} + \frac{1}{2(a-is)} \]Once there, merging the fractions together would yield:\begin{align*} \mathcal{L}\{\sin(at)\} & = \frac{2(a-is)-2(-a-is)}{-4 (a-is)(-a-is)} \\ & = \frac{2a-2is + 2a+2is}{4 (a^2 + isa-isa + s^2)} \\ & = \frac{4a}{4(a^2 + s^2)} \\ & = \frac{a}{a^2 + s^2} \end{align*}which shows that after Laplace transform, a sine is turned into a more tractable geometric function. By following similar reasoning, the Laplace transform of cosine can be shown to be equal to the following expression as well: \[ \mathcal{L}\{\cos (at)\} = \frac{s}{a^2 + s^2} \qquad (\mathrm{Re}(s) > 0) \] But then, one might argue “Why do we need to transform trigonometric functions like this when we can just integrate them?”
Diverging Functions: What the Laplace Transform is for
What if we throw a wrench in there by introducing a diverging function, say, $f(t)=e^{at}$? As it turns out, the Laplace transform of the exponential $e^{at}$ is actually deceptively simple: \begin{align*} \mathcal{L}\{e^{at}\} & = \int_0^{\infty} e^{at}e^{-st} \, dt \\ & = \int_0^{\infty} e^{(a-s)t} \, dt \end{align*}Here, we see that so long as $\mathrm{Re}(s) \gt a$, we would get that: \begin{align*} \int_0^{\infty} e^{(a-s)t} \, dt & = \left. \frac{e^{(a-s)t}}{a-s} \right|_0^{\infty} \\ & = 0-\frac{1}{a-s} \\ & = \frac{1}{s-a} \end{align*} That is, as long as $\mathrm{Re}(s) > a$, the Laplace transform of $e^{at}$ is a simple $1/(s-a)$. Here’s a video version of the derivation for the record.
On the other hand, if we mix the exponential $e^{at}$ with the power function $t^n$, we would then have: \[ \mathcal{L}\{t^n e^{at}\} = \int\limits_0^{\infty} t^n e^{at} e^{-st} \, dt \] which, after a bit of recursion and integration by parts, would become:\[ \frac{n!}{(s-a)^{n+1}} \]Here, notice how the transforms of exponential and power function are both represented in the expression, with the factorial $n!$, the $1/(s-a)$ fraction, and the $n + 1$ exponent.
In fact, it turns out that we can integrate any function with the Laplace transform, as long as it does not diverge faster than the $e^{at}$ exponential. In the tables of Laplace transforms, you might have noticed the $\mathrm{Re}(s) \gt a$ condition. That is what the condition is alluding to.
A Transform of Unfathomable Power
However, what we have seen is only the tip of the iceberg, since we can also use Laplace transform to transform the derivatives as well. In goes $f^{(n)}(t)$. Something happens. Then out goes:\[ s^n \mathcal{L}\{f(t)\}-\sum_{r=0}^{n-1} s^{n-1-r} f^{(r)}(0) \]For example, when $n=2$, we have that:\[ \mathcal{L}\{f^{\prime\prime}(t)\} = s^2 \mathcal{L}\{f(t)\}-sf(0)-f'(0) \]In addition to the derivatives, the $\mathcal{L}$ can also process some integrals: the integral sine, cosine and exponential, as well as the error function — to name a few.
But that’s not all. There is also the inverse Laplace transform, which takes a frequency-domain function and renders a time-domain function.
In fact, performing the transform from time to frequency and back once introduces a factor of $1/2\pi$. Sometimes, you’ll see the whole fraction in front of the inverse function, while other times, the transform and its inverse share a factor of $1/\sqrt{2\pi}$.
This is as if the Kraken could restitute the boat intact — but only for a factor of $1/2\pi$.
The Laplace transform, even after all those years, never ceases to bring us awe with its power. Here’s a table summarizing the transforms we’ve discussed thus far:
| Function | Laplace Transform |
|---|---|
| $1$ | $\dfrac{1}{s}$ |
| $t$ | $\dfrac{1}{s^2}$ |
| $t^n$ | $\dfrac{n!}{s^{n+1}}$ |
| $e^{at}$ | $\dfrac{1}{s-a}$ |
| $\sin(at)$ | $\dfrac{a}{a^2+s^2}$ |
| $\cos(at)$ | $\dfrac{s}{a^2+s^2}$ |
| $t^n e^{at}$ | $\dfrac{n!}{(s-a)^{n+1}}$ |
| $f^{(2)}(t)$ | $\displaystyle s^2 \mathcal{L}\{f(t)\}-sf(0)-f'(0)$ |
| $f^{(n)}(t)$ | $\displaystyle s^n \mathcal{L}\{f(t)\}-\sum_{r=0}^{n-1} s^{n-1-r} f^{(r)}(0)$ |

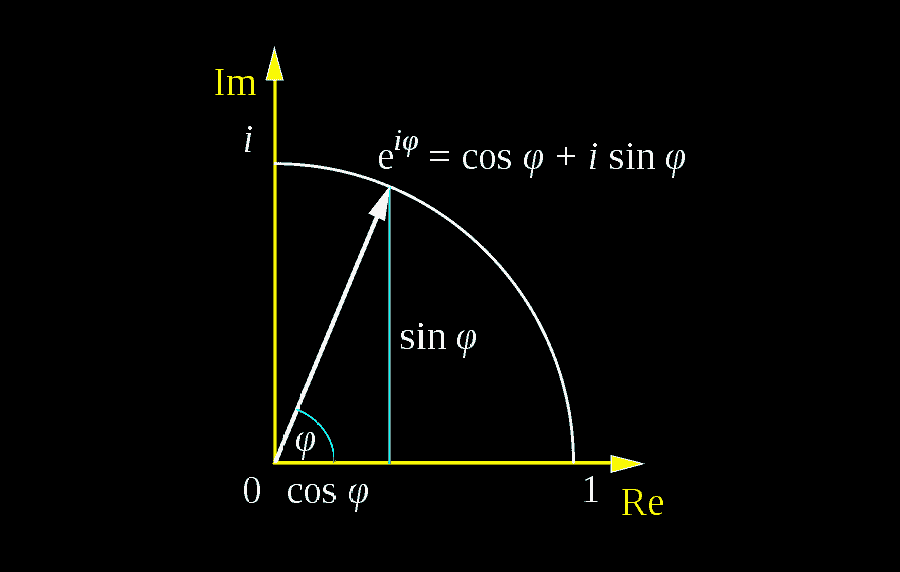

Any link to download soft copy?
Hi Amadi. Thanks for your interest. If you click on the “Print” button in your browser, you can save the guide as a PDF. That would be a way of generating a soft copy.