How to Solve the Triangle with A=30°, b=40, and a=10?

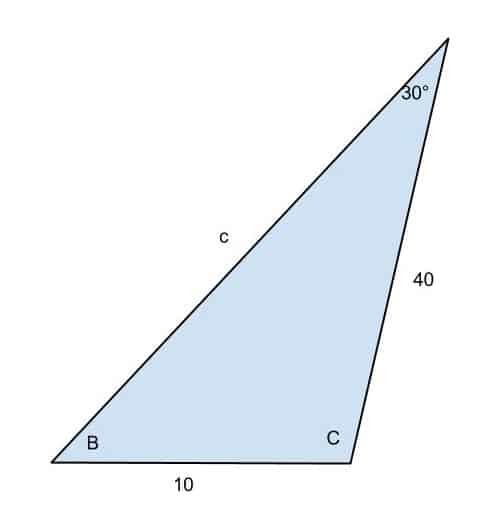
We got asked this trigonometry question, which we immediately converted into drawing for better readability.

Before we begin, what does it mean to solve a triangle? Well, it’s just a short way of saying finding all the missing side lengths and angles of a triangle.

So how on earth do we actually solve this triangle, with only 3 numbers given on the drawing? Well, that’s where some of our trigonometric tools can come into play…

Preliminary — The Law of Sines

There are many (Euclidean) triangles in this world, but regardless their measures and dimensions, one thing is for sure. Namely, given a triangle T, if you take any angle and calculate the ratio of its sine and its corresponding length, then you will always end up getting the same thing. To put it slightly differently, you can choose any angle from the triangle, calculate that ratio, and then — lo and behold — you always get the same ratio!

This theorem, which demonstrate an invariance of ratio in any triangle (i.e., not just the right triangles), is known as the Law of Sines. Mathematically, the Law of Sines asserts that:

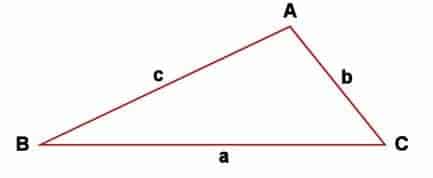
$$ \frac{\sin(A)}{a}=\frac{\sin(B)}{b}=\frac{\sin(C)}{c}$$

In practice, what this means is that once we manage to somehow calculate the ratio, having a known angle will allow us to deduce its corresponding side length, and vice versa (i.e., having a side length will enable us to calculate its corresponding angle as well).

Unsurprisingly, with the Law of Sines at hand, it’s not hard to see that once the ratio of the triangle is figured out, the other information about the triangle can also be deduced, one by one, pretty much like falling dominoes.

Testing The Water

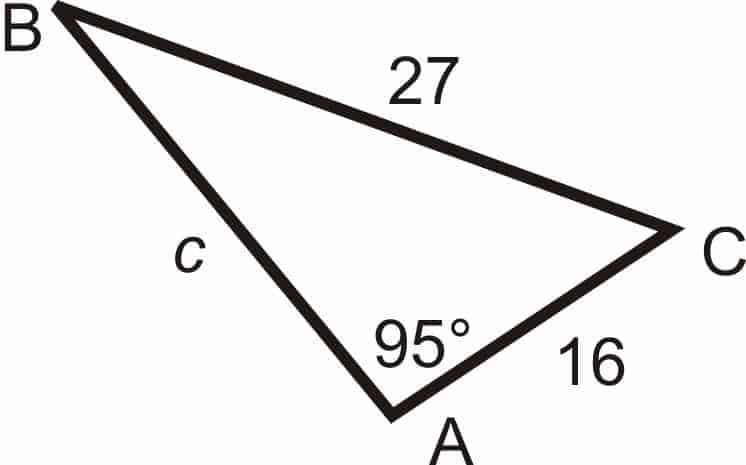Take this as our triangle for now. First, notice that we have the 95° angle and its corresponding length $27$, so the ratio of the triangle comes out fairly easily:

$$ \displaystyle \frac{\sin(95^\circ)}{27} \approx 0.0368961 $$

Second, notice that although we have neither $c$ nor $C$, we do have the side length $16$, which means that its corresponding angle can be deduced using the Law of Sines:

$$\frac{\sin(B)}{16} \approx 0.0368961$$

which means that:

$$\sin(B) \approx 0.59$$

Or equivalently:

$$B \approx \sin^{-1}(0.59) \approx 36.181^{\circ}$$

And now we do have $C$, which is $180^{\circ} – 95^{\circ} – 36.181^{\circ} \approx 48.819^{\circ}$.

The last measure to figure out would be $c$, which — since we have its corresponding angle $C$ — can be deduced using the Law of Sines again:

$$ \displaystyle \frac{\sin(48.819^{\circ})}{c} \approx 0.0368961$$

which means that:

$$ c = \frac{\sin(48.819^{\circ})}{0.0368961} \approx 20.4$$

As we can see here, the Law of Sines is pretty standalone in and of itself. Sure, we could have invoke the Law of Cosines to figure out $c$ near the end, but it’s definitely not needed. In fact,in the cases where we are given 2 angles and one side only, the Law of Cosines alone actually won’t solve anything!

Cracking Our Original Triangle

Time to go back to our question. First of all, notice that we have the 30° angle and its corresponding side length 10, so the ratio of the triangle comes out easily:

$$ \frac{\sin(30^{\circ})}{10}= 0.05$$

So the ratio is now determined. Shifting gears. Notice that we have a side length of $40$, and that alone with the ratio allows us to determine its corresponding angle:

$$\frac{\sin (B)}{40} = 0.05$$

which means that:

$$ \sin(B) = 2 $$

Hmm…What’s happening here? Nothing! It’s just that since sine of an angle ranges from $-1$ to $1$, $B$ cannot be possibly solved. In other words, the triangle you are seeing actually doesn’t exist (as an Euclidean entity that is)! And the “ratio” thing is literally coming out of thin air!

Now, that would make a damn good exam question, wouldn’t it? 😉