
If you’re of the type who enjoys playing around with graphing calculator, then you might be interested in the so-called Desmos Art. These are basically pictures and animations created in Desmos primarily through the clever use of equations and inequalities — among other features such as tables, animating sliders and regression models. Indeed, if you go to this official staff pick page, you should see that a whole bunch of creative artworks were already being created — anything from cartoon characters, landscape to logos and portraits.
But here’s a problem: when you reach a Desmos artwork page, you get to see the end-result with all the equations and inequalities, without necessarily having any clue about how the sketching process comes about from the beginning to the end:
- Why does this weird-looking equation pop out from nowhere?
- How did the author know that $3.982$ is the leading coefficient to use?
- And how did those numbers get so precise up to four decimals digits?
To remedy this situation, we came up with a laborious and interesting solution: we decided to go out there and create a new Desmos sketch from scratch, and work backward to comment a bit on the steps, procedures and reasoning involved in the sketching process — as we go through the different stages and portions of the drawing.
And with that, let’s proceed straight into our Desmos Art guide in computational sketching, which — as you might have guessed — is going to be both fun and informative — even if you have no intention whatsoever of using any graphing calculator in the near future.
Table of Contents
Step 1: Initial Setup — Source Picture
Unless you are some kind of sketching guru — which we certainly are not — it’s generally better to base the sketching on some underlying model: some picture that you actually want to draw; some picture that you can rely upon in case the sketching derails by a huge margin.
And in case it’s not clear enough, you should only choose a picture that you really, really enjoy sketching — something that you can derive a whole lot of satisfaction from. This is because unlike ordinary pencil-and-eraser sketching, sketching in Desmos has to be done by filling the command lines with equations, tables and inequalities, so that if you can’t fuel enough passion into a drawing, then the time and effort invested into reproducing it is probably not going to worth it.
Also, when choosing a picture, take good care to select one that is not too difficult to draw. Otherwise, you might have to regret your decision much later when you’re already, say, 21 hours into the process. Of course, you don’t want to make the picture too easy either, as it might not be much of a gratifying experience if you do it that way.
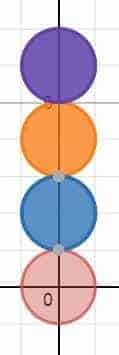
In our case, using the Reddit Gold membership recently awarded to us, we went out there and created our first very own signature Reddit alien avatar:

For the lack of better terms, let’s just call these lovely creatures Math Vault Redditlady and Redditdog, respectively. Now, does this logo make a good choice as a source image? We certainly think it does:
- Passion Level: Since we only create avatars that we like, channeling energy into recreating the creatures invented in part by ourselves is definitely not an issue.
- Complexity: Both the Redditlady and the Redditdog have very well-defined borders and colors, making it a formidable challenge that’s not too intimidating.
And with both criteria passed, we proceed to happily import our avatar image into Desmos. By default, Desmos likes to set the origin $(0,0)$ as the center of the image, and that is a good choice for most purposes. However, depending on the size of the source image, sometimes it makes sense to consider rescaling it so that at the default zoom level, the image occupies around 70% of the graphing grid either in height or in width. If the image is too small, then it’s hard to appreciate any fine detail, and if it’s too big, then one might have a hard time focusing on the big picture — literally.
In our case, since the avatar is just about the right size to start with, we decided to keep the dimension of the image to the default $10 \times 10$ setting at the end. We also didn’t alter the image’s aspect ratio either, which in many cases aren’t really necessary anyway.
But just to drive the message home a bit, setting up a source image correctly from the get-go is more important than it seems, since the last thing we want to be doing is to, say, rescale the image to an appropriate size after being already halfway through the sketching process.
Step 2: Divide and Conquer
How do you deal with a huge task that seems impossible to complete? You partition the task into smaller subtasks. That is, tasks that are so small that you actually enjoy doing them!
In particular, when it comes to sketching in Desmos, you want to section the picture into different portions, each of which can be finished in a reasonable amount of time, so that when it comes to the time of sketching, you focus on one single portion and one single portion only.
In our case, since we know that sketching the entire Redditlady and its companion pet can be quite a challenge, instead of resorting to despair, we divide the entire avatar into 6 portions — from the top to the bottom:
- Hat & Antenna
- Face
- Armor
- Hand & Rubik’s Cube
- Skirt
- Redditdog
By inspection, while we see that most of these portions are relatively simple to implement, we still anticipate some challenges ahead of us when it comes to the Armor portion. In an attempt to make the Armor less intimidating, we proceed to subdivide it further into 7 subportions:
- Left Shoulder
- Right Shoulder
- Collar
- Arm
- Chest
- “Lungs”
- “Outer Lungs”
With the gist of our organisational structure now settled, we then proceed to create a Desmos folder for each of the general portions, all of the while making a mental note that every command line pertaining to a specific portion should be dragged into its associated folder — if it’s not already in there.
And while Desmos doesn’t really support folder nesting at this point, there’s nothing preventing us from using comment lines to provide labels for the subportions. True, while this level of organization could be an overkill for a simple picture, as the complexity of the picture increases, structuring the command lines this way can make line identification and future reference substantially easier.

In our case for example, the need for quick reference became so urgent that towards the end of the sketching, we ended up creating far more subportions than we originally thought needed. Here’s our updated organisational structure at the completion of the avatar:
- Antenna & Hat
- Face
- Eyes
- Borders
- Armor
- Shoulders
- Collar & Arms
- Chest
- “Lungs” &”Outer Lungs”
- Hands & Rubik’s Cube
- Hand
- Right Side
- Left Side
- Top
- Skirt & Legs
- Coloring
- Gap
- Borders
- Legs
- Redditdog
- Face
- Ears
- Lower Body
- Body Gaps
- Leg Gaps
- Left Eye
- Right Eye
- Nose
- Tail
(Yep. The Redditdog proved to be a bit more annoying than originally anticipated. Hence the saying “Don’t judge a puppy by its cover.”)
Step 3: Portion Crunching
As mentioned a bit earlier, when working on a sketch, it’s often less intimidating to just focus on a portion while ignoring the rest. We call this portion crunching, and is done in part to ensure that the work completed with minimal resistance and mental blocks. In Desmos, portion crunching usually boils down to the following two parts: curving drawing and region coloring.
Step 3a: Drawing Curves
In general, a self-contained portion of an image is composed of close figures, which in turn can be construed as a series of curve segments. However, since these curve segments tend interact with each other, it would be hard for us to draw these segments sequentially — as would be done in ordinary pencil-and-eraser sketching. Instead, we prefer to resort to the strategy as outlined below:
- Model a curve segment using an appropriate class of equations, and leave its graph with the full domain intact.
- Do the modeling for each of the curve segments in the close figure.
- Cut off the excessive parts of each curve — by imposing restrictions on the associated equation.
In particular, we want the curve trimming to happen at the very end, because once the curve modeling are done for each curve segment in a close figure, Desmos will map out all the intersection points along with their coordinates — the latter of which provide key information as to where to cut off the curves, and might not be available had we decided to trim the curves off from the get-go.
In actuality though, we’ll probably spend more time modeling the curve segments rather than trimming them — as there are simply too many curves in too many different shapes and forms. And while it might be hard to provide an exhaustive set of tips for modeling each curve segment we will ever encounter, the following procedures should be more than enough to take care of most of them.
Modeling Line Segments
Many close figures are composed of nothing but lines, and vertical/horizontal line segments are about as easy as one can get. For example, to create the line segment connecting $(1.2, 5)$ with $(1.2, 5.67)$, simply typing $x=1.2 \, \{5\le y \le 5.67 \}$ into a command line will do just fine.
In general, if you know the coordinates of the two endpoints of a line segment, then you can enter them into a Desmos table, and re-configure the points (via the Gear Icon) to have a line segment passing through it.
On the other hand, if you only have the coordinate of a single point on the line segment, say $(2.33,4.67)$, then you can still resort to the point-slope form, which in this case becomes $y=(x-2.33)+4.67$. In fact, by simply adjusting the slope one digit at a time, and observing the graph at an ever-increasing zoom level, it shouldn’t take long to obtain a line that reasonably overlaps with the segment you are trying to model.
Modeling Circular/Elliptical Segments
In some cases, the borders of objects (e.g., eyes, ring, hands) are either ellipses themselves, or can modeled using some elliptical arcs. In which case, the following modeling procedure could be useful:
Procedure for Modeling Elliptical Segments
- For a full circle or a full ellipse, use the general equation $\displaystyle (x-h)^2+(y-k)^2 = r^2$ (resp., $\displaystyle \frac{(x-h)^2}{a^2}+\frac{(y-k)^2}{b^2}$$=1$) in the command line. If the circular/elliptical segment is already part of the top-half, bottom-half, left-half or right-half of a circle/ellipse, then use the corresponding function instead — this is vital if the region is to be colored later on.
- Don’t worry about which numbers to use for the parameters $r$, $a$, $b$, $h$ and $k$ yet. Just put in some numbers into the command line so that the resulting graph is reasonably close to the segment being modeled.
- Start by tweaking the radius $r$ (or in the case of ellipse, the radii $a$ and $b$) so that the resulting graph looks “parallel” to the segment being modeled. Do it one decimal at a time, before zooming in and moving onto the next decimal.
- Once satisfied, adjust the center of the circle/ellipse $(h,k)$ to where you think it should be. Try to nail in the accuracy one decimal at a time, and zoom in the graph repeatedly as you get better and better fit.
- Repeat Step 3 and Step 4 in that order — if needed to.
Modeling Other Curvy Segments
While elliptical segments tend to be curves with a rather pronounced curvature, there are other curve segments such that — while still curvy in their own way — does not posses this distinct characteristic. In which case, what we’ve found is that by modeling them using “polynomials”, it’s possible to sneak in some reasonable fit most of the time.
For example, to model a concave-up, increasing curve segment with a vertex close to, say, $(1.56,6,78)$, we can start with the vertex form $y = (x-1.56)^2 + 6.78$. And if the segment has a slower increase in the beginning but a faster increase in the end, the vertex form of a quartic function — say $y=(x-1.56)^4 + 6.78$ — can be used as a starting point instead.
In fact, by adjusting the “degree” of the “polynomial” to any other positive real number, we can provide a reasonable fit to a surprising number of curvy segments as well:
- For a U-curve segment, degree $4$ or more usually works wonder.
- For a concave up, line-like segment, a degree between $1$ and $2$ seems to be more appropriate.
- For a concave-down, increasing curve segment, a degree between $0$ and $1$ can be used instead.
In fact, by applying horizontal or vertical reflections (e.g., $-(x-1.56)^4 + 6.78$, $[-(x-1.56)]^{1.5} + 6.78$) to a “polynomial” vertex form, we can usually bend the resulting graph to any direction we want. This flexibility would result in the following procedure for modeling non-elliptical curve segments in general:
Procedure for Modeling Other Curvy Segments
- Type in the appropriate “polynomial” vertex form — up to the horizontal/vertical reflection — into the command line. The polynomial can be either a function of $x$ (which opens upwards or downwards), or a function of $y$ (which opens leftward or rightward).
- Don’t worry too much about which coordinates to use as the vertex at this point. As long as the resulting graph is reasonably close to the segment being modeled, it should be fine.
- Determine the degree of the “polynomial” that produces a graph most similar to the curve segment — by tweaking the number one decimal at a time.
- Determine the leading coefficient of the “polynomial” that makes the resulting graph most “parallel” to the segment being modeled— again by tweaking the number one decimal at a time.
- Once satisfied, correct the coordinates of the vertex so that the resulting graph overlaps with the curve segment being modeled. If any minor discrepancy is found, repeat Step 3, Step 4 and Step 5 — in that order.
Subdividing Curve Segments
In some occasions, a curve segment can be a bit convoluted that it’s simply easier to subdivide it into multiple curve segments instead (as opposed to using higher-order polynomial regression). For example:
- A round corner can be conceived as three curve segments, consisting of the two surrounding lines and a quarter-circle for the edge.
- The top portion of a mustache can sometimes be broken down into two elliptical segments.
- The tail of a pet can sometimes be made into a series of line/curve segments, and perhaps with a half-circle reserved for the tip of the tail.
In general, a curve segment can be cut by visualizing vertical lines in between. In which case, we can model the resulting subsegments individually as functions of $x$ — and if needed to — group these functions together again by defining a piecewise function in terms of $x$. Alternatively, a curve segment can also be cut by visualizing horizontal lines in between. In which case, the resulting subsegments can be modeled individually as functions of $y$ instead.
(For more on defining piecewise functions in Desmos, see Desmos: A Definitive Guide on Graphing and Computing.)
Curve Trimming
Once we finish modeling all the curve segments in a close figure, we can begin to trim off the excessive parts of each modeling curve by imposing restrictions on the associated equation. For most purposes, this is usually done by specifying the lower/upper bounds within which the curve is supposed to occur. For example:
- If a half-circle is only to be graphed when $x$ is between $2.57$ and $13.534$, then adding the clause $\{ 2.57 \le x \le 13.534 \}$ to the end of its equation will achieve the desired effect.
- If a U-curve is only to be displayed when $y$ is between $-2.3$ and $1.87$, then adding $\{ -2.3 \le y \le 1.87 \}$ to the end of its equation will take care of it.
As alluded to a bit earlier, the actual numbers for the upper/lower bounds are usually part of the coordinates of some intersection point. which can be displayed up to four decimals if you zoom in hard enough before clicking on them. In the case where an upper/lower bound doesn’t occur at any of the key points, the bound will have to be obtained manually by clicking a bit on the region where the curve is supposed to be trimmed off.
In some occasions (such as the case with an obliquely-trimmed ellipse), a simple upper/lower bound simply won’t be enough to cut the curve the right way. Instead, you will have to define the upper/lower bounds as actual functions (either in terms of $x$ or in terms of $y$), and use them accordingly in the restriction clauses. In other occasions, you might even have to stack up multiple restriction clauses in order to get the desired effect.
Step 3b: Coloring Regions
After modeling and trimming all the curve segments in a close figure, it’s about time to start thinking about coloring the region inside. For implicit equations such as that of a full circle or an ellipse, this can usually be done by replacing the $=$ sign in the equation with the $\le$ sign. In most likelihood though, coloring a region is not going this easy, as many close figures have an irregular area that is bounded by a series of different-looking curve segments instead.
For example. in the case where an irregular area occurs but has rather well-defined upper and lower bounds, the coloring is usually done using the procedure below:
- Define the upper bound of the region as a function of $x$ (let’s call it $g(x)$). If the upper bound consists of multiple curve segments, then the function will have to be defined piecewise in order to take into account all the segments involved.
- In a similar manner, define the lower bound of the region as a function of $x$ as well (let’s call it $f(x)$ for now).
- Color the region by entering the inequality $f(x) \le y \le g(x)$ into a command line.
In some occasions, it might not be possible to color a region using $y$ as the bounded variable. If that’s the case, then you might have to adjust the above procedure to use $x$ as the bounded variable instead (e.g., color the region via an inequality of the form $f(y) \le x \le g(y)$).
In Desmos, if you color a region using a single inequality, the coloring will usually be a bit on the paler side. To increase the depth of the coloring, one thing you can do is to simply duplicate the same inequality three or more times in the command line. In fact, if you have some knowledge in color mixing, then you should play around with the different color combinations a bit and see what kind of end result you get!
Portion Crunching in Action: Antenna & Hat
So, how exactly does portion crunching work out in practice? To figure that out, we thought we would elaborate a bit on how we manage to crunch out the Antenna & Hat portion of our avatar.
First of all, we would start by subdividing the antenna into several sections, and modeled them individually using a series of functions:
- Antenna Ring: This is simply modeled using two full circles.
- Antenna Cable (Upper Part): Being more like a round corner, the cable is segmented and modeled using a line, a half-circle and another line joining the ring to the hat.
- Antenna Cable (Lower Part): This is simply modeled using two lines.

As for the hat, here’s what we did:
- Hat Disks (Top and Bottom): Sorry. We cheated. Each of the disks is modeled after an rotated ellipse, which takes on a slightly more involved equation.
- Hat Borders (Vertical): These are simply modeled after two oblique lines.
- Hat Mid-lines (Horizontal Curves): These are modeled using quadratic functions in vertex form.
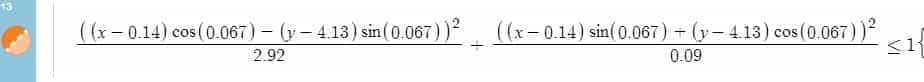
And with the modeling all done, we’re left with a bunch of curves that intersect each other. Using the coordinates of these intersection points, we proceed to trim off the excessive parts of the curves one by one:
- Outer Circle (Antenna Ring): This circle needs to have a gap on the upper-left end, so we trimmed off the excess by:
- Defining a linear function connecting the endpoints of the gap (let’s call it $f(x)$ for now).
- Appending the restriction clause $\{ y \le f(x) \}$ to the end of the equation of the outer circle.
- Antenna Cable: Each equation making up the antenna cable is trimmed off by imposing simple restriction clauses on $x$ (e.g., $\{0.6153 \le x \le 1.755 \}$), where the actual numbers for the upper/lower bounds are obtained through the coordinates of the intersection points.
- Hat: the equations for the vertical hat borders and the horizontal hat mid-lines are trimmed off in a similar manner — again using the relevant intersection points.
Once the curves are well-trimmed, we then proceed to color the different parts of the hat as follows:
- Top Disk: This is colored easily by changing the $=$ sign in the equation to $\le$.
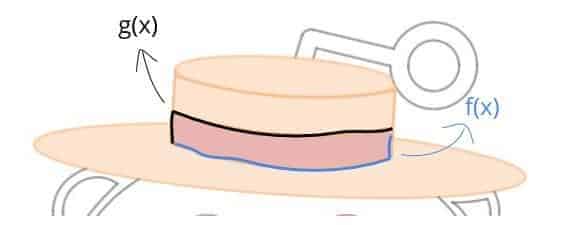
- Upper and Lower Strip: Each of the strip is colored using an inequality of the form $f(x) \le y \le g(x)$, where $f(x)$ and $g(x)$ are the lower and upper bound functions of the strip region, respectively, and both functions have to be defined piecewise (see the figure below for more).
- Bottom Disk: Since the Lower Strip is red and this part needs to be in orange, we color it by appending the restriction clause $\{ y\le f(x) \}$ into the equation of the ellipse.
All right. So that pretty much concludes the very first portion of our avatar! By the way, here’s a visual depiction of the upper/lower bounds for the red Lower Strip region — in case it still hasn’t clicked yet:
Step 4: More Portion Crunching
Once you run through all the hurdles of drawing a portion/subportion of your picture, it’s time to move on to other portions and put your new-found skills into good use. How? By picking a close figure, focusing on modeling the curves, trimming off the excess and coloring the figure, and before you know it, everything is set in front of your eyes!
(after 6 hours of undivided attention, for example)
However, there’s a caveat: for many aspiring Desmos artists, this advice doesn’t seem to be particularly actionable. If that’s you, then you’ll definitively find the following tips and strategies we used to sketch the other portions of the avatar a bit more informative.
Redditlady’s Face
As expected, we find the face to be one of the easiest portions to sketch, since most of the curve segments involved are either full circles themselves, or parts of a circle/ellipse:
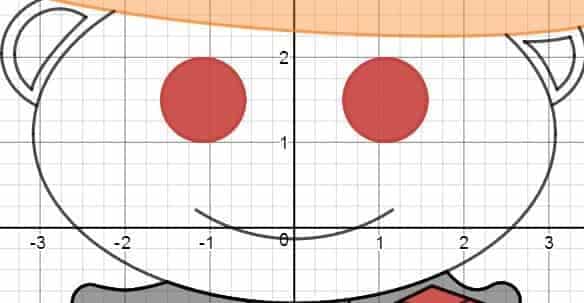
- Eyes: As round as they are, these eyes can be easily modeled using full circles. Indeed, with just a bit of parameter tweaking, it didn’t take long before we figure out the radius and the center of the circle, which is then colored by changing the $=$ sign in their equation to $\le$. The resulting inequalities are then duplicated several times to increase the depth of the coloring.
- Face Border & Smile: Being both elliptical segments in disguise, the face border and the smile are both modeled using full ellipses. The “smile” ellipse is trimmed off using the restriction clause $\{ y \le 0.202 \}$, while the face border had to be trimmed off using a custom-defined upper bound function on $y$ (the latter of which is defined as the line connecting the two points where the face and the hat intersect).
- Left Ear: The two outer circular arcs are modeled using full circles, while the innermost curve — which resembles a line — is actually modeled using the vertex form of a “polynomial” of degree $0.7$ (i.e., $c(x-h)^{0.7}+k$). Using the coordinates of the relevant intersection points provided by Desmos, the three resulting curves are then trimmed off by appending simple upper/lower bounds on their respective equations.
- Right Ear: The two outer arcs are now modeled after a full circle (inner arc) and a full ellipse (outermost arc), respectively. The two inner curves are not exactly elliptical in nature, so we modeled the top one using a quadratic vertex form ($0.24 (x-2.783)^2+2.188$ to be sure), and the bottom one using a “polynomial” vertex form with degree $2.7$ (after a bit of tweaking). Once there, by using the coordinates of the surrounding intersection points, we trimmed off the two outer arcs by imposing simple upper/lower bounds on both $x$ and $y$, and the two inner curves by appending simple restriction clauses on the value of $x$.
Hand & Rubik’s Cube
Being composed of simple geometrical shapes, we didn’t anticipate the Hand & Rubik’s Cube portion to be particular hard either, and in retrospect, we were almost entirely right on that one:
Hand: These are basically just two standard full ellipses — with no trimming required.
Rubik’s Cube (Left and Right Side): Since this part is composed entirely of lines, we basically went point-slope form all the way through. In addition, since the vertical-looking lines here are indeed vertical, it didn’t take a lot of tweaking to finish this part.
Rubik’s Cube (Top Side): Same drill. Except that all the lines are now oblique, hence literally point-slope form all the way through.
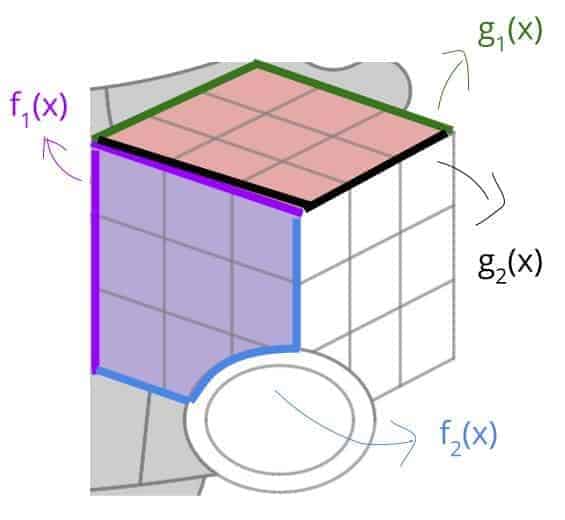
So all seems to go well, until it came the time to color the cube that is! As you can see in the left figure, the red portion is colored by defining $g_1(x)$ and $g_2(x)$ as the upper and lower bound functions, and by using the inequality $g_2(x) \le y$ $\le g_1(x)$ — which is duplicated five times in the command line to provide that reddish tint.
(by the way, these are not the actual names we gave to those functions, but it helps to think of them that way.)
In a similar manner, the left side of the cube is colored by restricting the $y$-values to be between $f_2(x)$ and $f_1(x)$ — both of which had to be defined piecewise. For example, the lower bound function $f_2(x)$ had to be defined by conjoining the left vertical line segment, the top-half of the ellipse, and the right vertical line segment — in that order. This of course means that the original equation of the full ellipse had to be reduced to a function first — before we can used it to define a piecewise function.
So in overall, while the coloring process did get a bit involved in the end, sketching the Rubik’s cube in Desmos is kind of cool in itself, as it exemplifies how a 3D figure can be reproduced on a 2D interface — with equations and inequalities even!
Skirt & Legs
While this portion might look simple at the first sight, it is actually a bit sticky as there are many different kinds of curve segments involved. But nevertheless, let’s have the picture do the talk for us first:
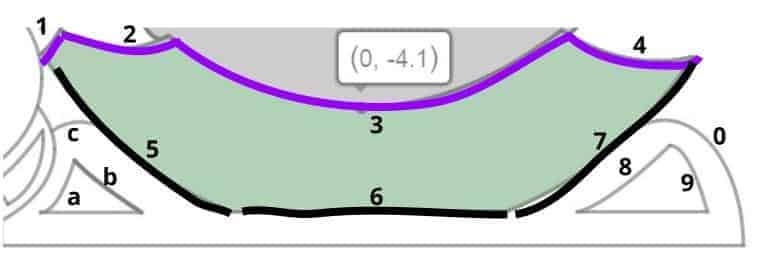
As can be seen above, the skirt alone is surrounded by seven curve segments, where:
- Curve 1 is modeled using the bottom-half of an ellipse.
- Curve 2, 3 and 4 are modeled after quadratic vertex forms.
- Curve 6 is just a horizontal line — nothing fancy here.
- Curve 5 and 7 are both parts of the bottom half of the same ellipse.
With these seven curve segments modeled, we then use the coordinates of the resulting intersection points to trim the curves into the right length. After which, we proceed to define the upper bound function $g(x)$ by conjoining Curve 1,2,3 and 4, and the lower bound function $f(x)$ by conjoining Curve 5, 6 and 7. The skirt is then colored green using the inequality $f(x) \le y \le g(x)$, which is duplicated three times in the command line to make the skirt a bit greener.
As for the legs, we’ve decided to sketch them using the following modeling scheme instead:
- Curve
cand Curve 0 are both modeled after the top-half of an ellipse. - Curve
ais modeled using a quadratic vertex form, while Curveb— which looks more like a “curvy line” — is modeled using a “polynomial” vertex form with degree $0.8$. - Curve 8 and 9 got a bit more subtle, so we chose to model them using “polynomial” vertex form as well. After a bit of tweaking, we found that Curve 8 — which looks like an intermediate function between a line and a parabola — can be modeled fairly well with degree $1.35$. As for Curve 9, we’ve found a match when the degree is $1.99$
(Yep. Looks like we’ve “curved” it a little bit.)
Redditdog
Remember us complaining about the Redditdog? Well, it’s about time to figure out just how annoying it was!
Ears & Beyond

The subportion we’re looking at here are the tail and the ears. As surprising as it seems, we didn’t model the tail using a bunch of lines and half-circles (which we probably should have). Instead, we decided to model the left and right sides of the tail using hyperbolas, and the tip of the tail using the top-half of a circle.
And yes, we had to do some serious zooming and number tweaking to make sure that the parameters were robust enough, and that we can actually glue the tail together without any human noticing. But that still doesn’t change the fact that the tail is really three segments in one. Not good if you are this dog of course! 🙂
As for the ears, since all the four outer borders are pretty curvy, we decided to modeled them after the top-half/bottom-half of an ellipse. On the other hand, because the inner borders are much less curvy than the outer ones, we decided finally to use “polynomial” vertex forms on them instead.
Face

All right. Let’s take a look at how we dealt with this, hmm… dogface:
- Face Border: This is just a plain-old full ellipse — with no trimming required.
- Eyes: Unlike the Redditlady, our Redditdog’s eyes are not exactly made of full circles. As such, we have to take into account of the line segments in the upper-extreme corners when modeling the borders. In order to color the eyes, we define the upper bound function $g(x)$ piecewise by conjoining the line segment with the corresponding quarter-circle. We also define the lower bound function $f(x)$ as the bottom-half of the relevant circle. After which, each eye is then shaded red by duplicating the inequality $f(x) \le y \le g(x)$ three times.
- Nose: This is nothing more than a triangle, or more specifically, a horizontal line segment on the top followed by two oblique line segments at the bottom. Make sure you know by now how to sketch these segments and color the region within!
- Whiskers: Due to their curvy nature, we decided to model the whiskers after the bottom-half of a circle. In fact, since the whiskers are symmetric about a horizontal line, all we had to do is to work out the function for the right whisker, and apply a horizontal reflection to get the left one for free.
Body & Legs
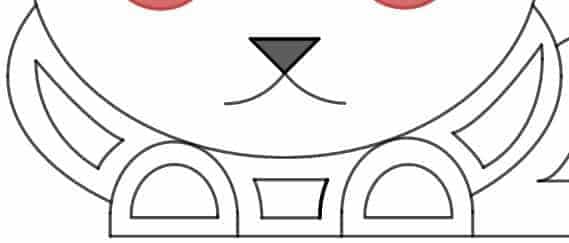
Apparently, someone on Reddit made sure that a lot of design go into a dog’s lower body. However, after a bit of trial-and-errors, we found that we were still able to model each of the curve segments using either a full ellipse, a half-ellipse, or a “polynomial” vertex form. For example:
- The two outermost curve segments on the left and right sides of the body can be modeled as full ellipses, which are then trimmed off by imposing simple restrictions on both $x$ and $y$.
- The remaining curve segments forming the left and right “triangles” — which are not as curvy than the ones above — are modeled after “polynomial” vertex form with varying degrees.
- The left and right “horseshoes” can be easily modeled using a combination of full ellipses and horizontal lines, each of which subject to some simple restriction clause.
- Similarly, the “trapezoidal” gap between the legs can also be modeled using a combination of half-ellipses and horizontal lines — which are again subject to some simple restriction clauses.
Redditlady’s Armor
As one would have guessed, the armor piece is probably the toughest portion we have had to deal with. To ease the sketching process, we divide it further into four subportions: the shoulders, the arm, the chest, and the “abdomen”.
Shoulders
First, here’s a graphical depiction of the breakdown of the shoulders and the “collarbone”:
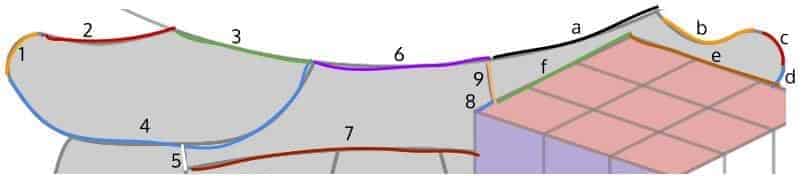
As you can see, the curve segments here start to get a bit into the crazy zone. The left shoulder, for example. is colored by using Curve 1, 2, 3 jointly as the upper bound and Curve 4 as the lower bound. Curve 1 — being the round edge of the shoulder — is modeled after the top-half of a circle, while Curve 2 and Curve 4 are modeled using “polynomial” vertex forms (with degree $1.6$ and $4$, respectively). On the other hand, Curve 3, which is a part of the face border, had to be remodeled as the bottom-half of an ellipse — by recycling the equation of the full ellipse which was previously used to model the face border.
In a similar manner, we also colored the right shoulder grey by using Curve a, b, c jointly as the upper bound, and Curve 9, f, e, d as the lower bound, except that this time, the curve segments are modeled using a combination of lines (Curve f and e), half-circles/ellipses (Curve b, c and d) and “polynomial” vertex forms (Curve 9 and b). In fact, a similar modeling and coloring scheme applies to the “collarbone” area as well.
Arm
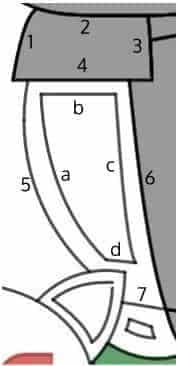
Looking at the figure on the left, we see that the arm is a relatively easy portion to implement. For example:
- The sleeve can be colored grey using an inequality of the form $f(x) \le y \le g(x)$, where $f(x)$ is the horizontal line used to modeled Curve 4, and $g(x)$ is the piecewise function formed by conjoining Curve 1,2 and 3 — all of which can be modeled after “polynomial” vertex forms.
- The two outer curve segments for the arm (i.e., Curve 5 and Curve
a) are actually elliptical arcs, and thus are modeled after full ellipses. - On the other hand, Curve
cand Curve 6 — which are a bit more linear in nature — had to be modeled using “polynomial” vertex forms of low degree instead. - The other remaining curves are just line segments, so it didn’t take us a long time to reproduce them.
Chest
OK. Here comes the inevitable part: the chest. To begin, here’s a graphical depiction of most of the curve segments involved:
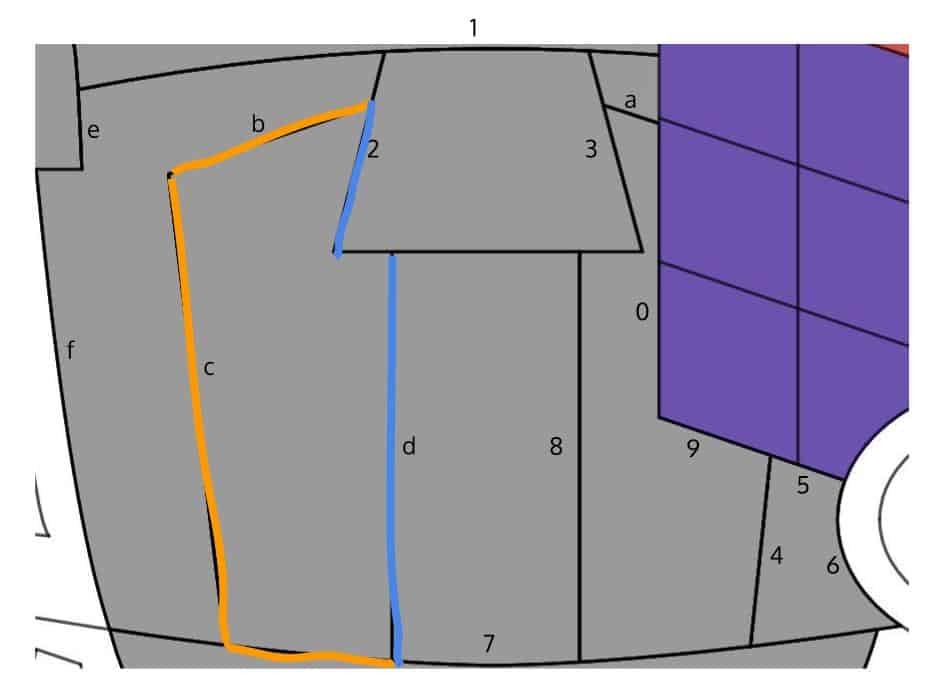
By inspection, the easiest part is probably the “tie” area in the middle, since it’s composed of a “trapezoid” on the top, and a “rectangle” at the bottom. To be sure, we did realize that neither Curve 1 nor Curve 7 are actually lines, so we took good care to model them using “polynomial” vertex forms instead.
After that, we moved on to the second easiest parts, which we determined to be the tiny “trapezoid” on the upper-right, and the weird-looking region next to the hand. Why the second easiest? Because both regions can be colored using an inequality of the form $f(x) \le y \le g(x)$ — as long as we take good care in defining the upper and the lower bound function $f$ and $g$ to take into account all the relevant segments involved.
Now, here comes the sticky part: if you look at the region in the above figure that is enclosed in orange and blue, then it shouldn’t take long to realize that it would be difficult to color this region using standard inequalities of the form $f(x) \le y \le g(x)$. In fact, if you decide to stubbornly stick with this route anyway, then you will end up “scratching” our Redditlady’s armor with a few unsightly little patches!
Instead, what we want to do is to color the region using an inequality of the form $f(y) \le x \le g(y)$, where the lower bound function $f(y)$ is defined by conjoining the relevant part of Curve 7, Curve c and Curve b, and where the upper bound function $g(y)$ is defined by conjoining Curve d with the relevant part of Curve 2. Basically, $f(x)$ corresponds to the curve in the above figure that is outlined in orange, and $g(x)$ the part in blue.
In fact, by using the same strategy, the two remaining areas in the chest region — the right “lung” and the left “outer lung” that is — can also be colored using a single inequality as well.
“Abdomen”
All right. We’ve come to the last part, which is not too bad either — especially after going through the nitty-gritty of that Chest portion.
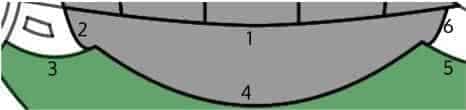
In a nutshell, we basically colored the abdomen in grey by using a standard inequality of the form $f(x) \le y \le g(x)$, where:
- $g(x)$ is the function we used to model Curve 1 (a “polynomial” vertex form with degree $1.6$ to be exact — due to the linear nature of the curve).
- $f(x)$ is the lower bound function obtained by conjoining — in that order — Curve 2, the relevant section of Curve 3, Curve 4, the relevant section of Curve 5, and finally, Curve 6. Interestingly, each of these curve segments can be modeled using “polynomial” vertex forms — in particular as quadratic functions with varying slopes.
And guess what? We’re done! All the 219 equations/inequalities that is! Here’s a before-and-after picture for to be sure:

Granted, there’s still a lot of subtleties and nuances going into how each of the equations and inequalities are constructed. and that is why we’ve decided to reserve the best for last. Namely, if you’re still curious about all the technical details behind the sketch, then you should definitely go to our Redditlady’s Desmos page and take a look at those command lines yourself!
Closing Words
Wow! That was a lot of work and fun for us, so hopefully the same is true for you too. If anything, this is definitely graphic design of a different caliber — and with a wicked geeky twist even!
Indeed, sketching in Desmos is like drawing with two hands (or maybe the legs as well) tied, even though a voice deep inside us is saying that this is only good for the cause of mathematics. This is because by the time you become a Desmos sketching master, you would have acquired a solid intuition about various geometrical shapes and the corresponding equations/inequalities you can use to model them. Who knows. perhaps it might even improve your ability to evaluate a double/triple integral — if you ever decide to take the multivariate calculus route that is!
All right. Ready for the long-awaited interactive table? Because here it is!
- Step 1: Source Image
- Step 2: Divide and Conquer
- Step 3: Portion Crunching
- Step 4: More Portion Crunching
Make sure to go through the following checklist for your source image — before you have to learn things the hard way:
Passion Level
- Are you passionate enough about the picture you have chosen?
- Are you OK with injecting hours of time and effort into your picture, in order to create something you can be potentially proud of?
Difficulty Level
- Is the picture too easy to be deemed a fair challenge?
- Is the picture too intricate to be worth a try?
Image Scaling at the Default Zoom Level
- Does the image occupy about 70% of the graphing grid — either by width or by height?
- Ease the sketching process by dividing the image into multiple portions — each of which is to be managed using a Desmos folder.
- For each portion that is still relatively large to handle, divide it further into subportions that are reasonably manageable.
- While Desmos does not support folder nesting at this point, the subportions can still be managed using comment lines in Desmos.
General Procedure
In Desmos, curves are better drawn in groups by:
- Picking a close figure (or an otherwise self-contained figure).
- Modeling each of its curve segments using an appropriate class of equations.
- Trimming off the excessive parts of each curve by imposing appropriate restriction clause(s) to the equation of the curve.
Modeling Line Segments
- Vertical/horizontal line segments can be easily modeled using equations — along with some simple restriction clauses.
- A line segment can also be drawn in Desmos using a table of points — provided that the two endpoints are known.
- If only one point on the line segment is known, then the segment can still be modeled using point-slope form.
Modeling Circular/Elliptical Segments
- For full circles/ellipses, use the corresponding general equation.
- For curve segments which are parts of a half circle or a half-ellipse, use the aassociated functions instead.
- Tweak the radius parameter(s) first to get a curve that is as “parallel” to the segment being modeled as possible, before adjusting the coordinates of the center. Repeat the process as many times as needed.
Modeling Other Curvy Segments
- Use “polynomial” vertex form to model a segment with a less pronounced curvature.
- The “degree” of the polynomial can be any positive real number — the closer the degree is to $1$, the straighter the polynomial.
- Tweak the degree and the leading coefficient first to get a curve that is as “parallel” to the segment being modeled as possible, before adjusting the coordinate of the vertex. Repeat the process as many times as needed.
Subdividing Curve Segments
- If a curve segment is too intricate, we can further subdivide it using:
- Vertical lines (which produces subsegments that can be modeled using functions of $x$).
- Horizontal lines (which produces subsegments that can be modeled using functions of $y$).
Curve Trimming
Once all the curve segments of a figure are modeled, the excessive parts of a curve can be trimmed off by appending restriction clause(s) to the equation of the curve:
- Restriction on $x$ (e.g., $\{ 1.24 \le x \le 2.566 \}$)
- Restriction on $y$ (e.g., $\{ -23.15 \le y \le -5.69 \}$)
In general, the actual numbers for the bounds can be obtained from the coordinates of the relevant intersection points. In other occasions, one might have to stack up multiple restriction clauses to get the desired effect.
Implicit Equations
For regions such as that of an ellipse, a circle or a plane, the coloring can be sometimes done by changing the $=$ sign in the equation into $\le$.
General Coloring
In most cases, a region can also be colored by:
- Imposing bounds on the $y$-values (via an inequality of the form $f(x) \le y \le g(x)$).
- Imposing bounds on the $x$-values (via an inequality of the form $f(y) \le x \le g(y)$).
where the functions $f$ and $g$ stands for the lower and the upper bound of the region, respectively, some of which might have to be defined piecewise — by conjoining all the relevant curve segments together.
Really, just grind through each of the portions using the procedures introduced in Step 3, and you should be good to go!
And there you have it. The end of yet another intensely graphical saga with Desmos! Now, back to you: what kind of picture are you looking to draw with equations and inequalities? Either way, make sure to make use of what you’ve just learned on curve modelling so that when the time comes, you can draw like a real computational artist!



