Troubleshooting: Evaluating a Trigonometric Integral Algebraically

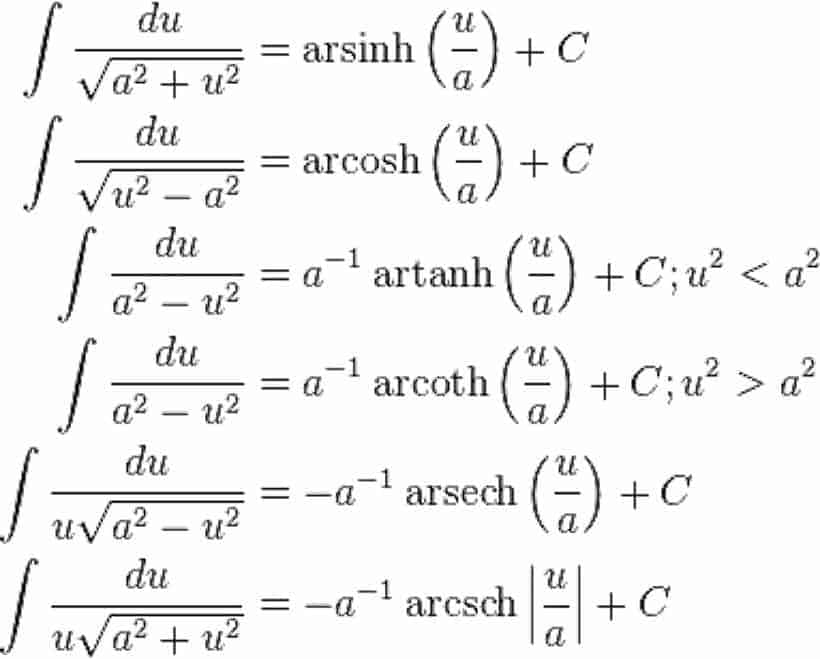
(For an integration method which can potentially substitute integration by parts and the substitution method itself, see The Overshooting Method.)

Yes. It can be sometimes amusing to see calculus students mis-integrating a function to the point of yielding nonsensical answers. To illustrate what we mean by this, here is Steve, who — at the point of this writing at least — still haven’t got a clue where his computations went awry:

How do you evaluate $\displaystyle \int_{-5}^5 x – \sqrt{25-x^2} \, dx$ algebraically? When I take the areas geometrically, I get $\displaystyle -\frac{25\pi}{2}$, as $\displaystyle \int_{-5}^5 x \, dx=0$ and $\displaystyle \int_{-5}^5 \sqrt{25-x^2} \, dx$ is the area of a half-circle with radius $5$. But when I try to evaluate it algebraically, I don’t seem to get the same answer: $\displaystyle \int^5_{-5}\left(x-\sqrt{25-x^2}\right)\,dx=\left[\frac{x^2}{2}-\frac{2}{3}(25-x^2)^{3/2}+C\right]^{5}_{-5} \dots$

OK…What’s going on here? Well, keep reading!

Integrating Root Functions

Well. $\displaystyle\int_{-5}^5 x-\sqrt{25-x^2} \, dx=\int_{-5}^5 x \, dx-\int_{-5}^5\sqrt{25-x^2}\, dx$. For the 2^nd integral, we can’t integrate it as if it were $\sqrt{x}$. In fact, if we try to “integrate” $\displaystyle\sqrt{25-x^2}$ this way, we get:

\[ \frac{2}{3}\left({25-x^2}\right)^{\frac{3}{2}} \]

However,

\[ \frac{d}{dx}\left[ \frac{2}{3}\left({25-x^2}\right)^{\frac{3}{2}} \right] = \sqrt{25-x^2}(-2x) \ne\sqrt{25-x^2} \]

Oops. Looks like the obnoxious Chain Rule just destroyed our whole scheme.

Troubleshooting: Our Answer

So is there a paradox? Not really. It’s merely an illustration of how the misuse of Power Rule can create abnormal antiderivatives. For the 2^nd integral, what we need to do is to use a back substitution with $x=5\sin(u)$. In which case, $dx=5\cos(u)du$, and the limits of the integral now run from $\displaystyle -\frac{\pi}{2}$ to $\displaystyle \frac{\pi}{2}$. Putting everything together, we get:

\begin{align*} \int_{-5}^5 \sqrt{25-x^2}\, dx =\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\sqrt{25-\left(5\sin(u)\right)^2} \ 5\cos(u) \, du \end{align*}

Simplifying further, we get:

\begin{align*} \displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}5\cos(u) \, 5\cos(u) \, du=25\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^2(u) \, du \end{align*}

By using the half-angle formula for cosine (i.e., $\cos^2 u =\left(1 + \cos(2u)\right)/2\,$), we can continue to work on the antiderivative:

\begin{align*} 25\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cos^2(u) \, du  & = 25\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1 + \cos(2u)}{2} \, du  \\ & = 25\left [\frac{1}{2}x+ \frac{\sin(2u)}{4}\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \\ & = 25\left(\frac{\pi}{2}\right) \end{align*}

which means that our original integral, $\large \displaystyle \int_{-5}^5 x – \sqrt{25-x^2} \, dx$, would be $\displaystyle -\frac{25\pi}{2}$, as Steve has previously inferred using a geometric argument.

And if there is a moral to this story, it would be that there would be no paradox at all — as long as we don’t go for an anarchic free-for-all! 😉

Some Calculus-Related Guides You Might Be Interested In

• Chain Rule for Derivative — The Theory
• Derivative of Inverse Functions: Theory & Applications
• Derivatives of $x^x$, $x^{x^x}$…
• Exponent Rule for Derivative: Theory & Applications
• Algebra of Infinite Limits and Polynomial’s End-Behaviors
• Integration Series: The Overshooting Method

How's your higher math going?

Shallow learning and mechanical practices rarely work in higher mathematics. Instead, use these 10 principles to optimize your learning and prevent years of wasted effort.

Hmm... Tell me more.