Derivative of Inverse Functions: Theory and Applications

Quick question. Are you currently (or have been) a student of differential calculus (a.k.a., Calculus I)? If so, maybe you can guess what is on that (potentially-cryptic) graph above?

What. Inverse functions of course! Just look at that beautiful shape and how well they correspond with each other!

(OK. Bonus point: can you guess which functions they are?)

Yep. There is definitely more than meet the eyes. Granted, inverse functions are studied even before a typical calculus course, but their roles and utilities in the development of calculus only start to become increasingly apparent, after the discovery of a certain formula — which related the derivative of an inverse function to its original function. And guess what? That — is the topic that we’ll be delving into in greater details today.

So… hang on tight there, as you are about to travel to the land of exotically-strange functions in a few seconds. 😉

A Primer on Inverse Functions

In theory, given a function $f$ defined on an interval $I$, the role of $f$ is to map $x$ to $f(x)$. That is, $x$ plays the role of the referrer, with $f(x)$ being the target of $x$.

Collectively, the set of all targets of $f$ under $I$ forms the set commonly known as $f(I)$ — or the image of $f$ under $I$ (think of the candle-and-wall analogy in optics). Under this terminology, the function $f$ is said to map $I$ to $f(I)$.

(For other basic function-related notations and terminology, see function-related symbols.)

Presumably, if another function can be constructed to map each target back to its referrer, then this new function would be considered the inverse function of $f$ — or $f^{-1}$ for short.

Of course. Not all functions can have inverse. However, for a certain class of functions that are deemed injective (i.e., functions where every referrer points to a different target), every target will have a unique referrer. This means that it would then be possible to define a function — which maps each target in $f(I)$ back to its original referrer in $I$. Such a function would then be rightfully considered the inverse of $f$.

In the context of functions involving real numbers (i.e., real-valued functions), the domains are usually a union of open or close interval, and in the context of calculus, the functions are generally assumed to be differentiable (and hence continuous). As it happens, when these assumptions are combined together, the results are a series of fundamental and increasingly powerful theorems about invertible functions:

A classic example illustrating these theorems would be the function $f(x)=x^2$. For example, when we take the domain of $f$ to be $\mathbb{R}$ (i.e., the set of all real numbers), the function $f$ would map both $-1$ and $+1$ to the same number, and is therefore not invertible. However, when the domain is restricted to the set of non-negative numbers, $f$ would now become injective everywhere, and hence is by extension invertible, with the inverse being the function $f^{-1}(x)=\sqrt{x}$.

Also, since $f$ is continuous and injective on the set of non-negative numbers, by Theorem 2 $f$ should be monotone (or as in this case — strictly increasing) on this domain, and since continuous injective functions produce continuous inverses, the inverse of $f$ — the square root function $\sqrt{x}$ — should be continuous (and strictly increasing) on its own domain as well — which it is!

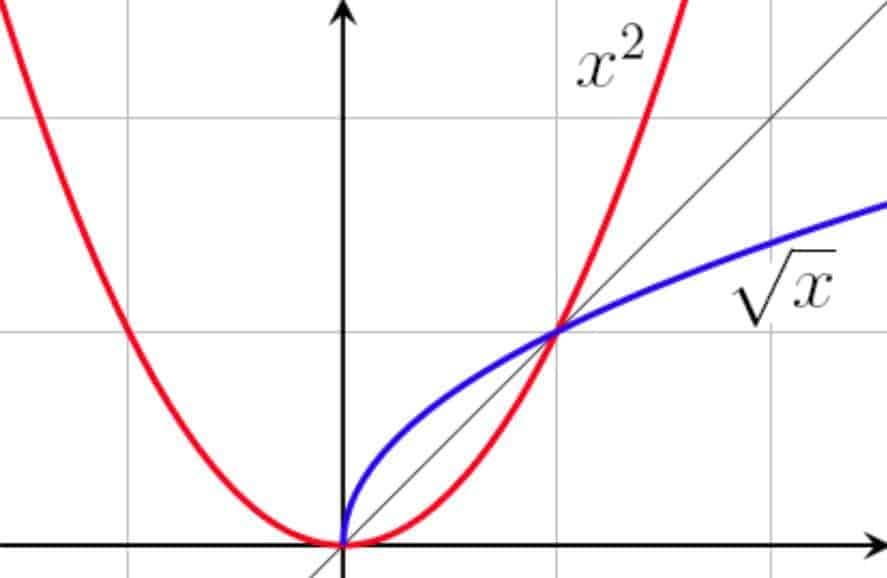
Note that in general, since the graph of $f$ is the set of points $(x,f(x))$ and $f^{-1}$ the set of points $(f(x),x)$, the two functions are — graphically speaking — mirror reflection of each other along the diagonal axis $f(x)=x$.

Alternatively, since $f$ is also the inverse of $f^{-1}$, one can also think of the graph of $f^{-1}$ as the set of points $(x, f^{-1}(x))$, and the graph of $f$ the set of points $(f^{-1}(x),x)$. Hence, it is fair to say — in our language at least — that $x$ and $f(x)$ are correlates of each other (from the perspective of $f$), much like the same way that $x$ and $f^{-1}(x)$ are correlates of each other (from the perspective of $f^{-1}$).

Derivative of Inverse Functions

As it stands, mathematicians have long noticed the relationship between a point in a function and its correlate in the inverse function. More specifically, it turns out that the slopes of tangent lines at these two points are exactly reciprocal of each other! To be sure, here’s a neat animation from Dr. Phan to prove our sanity:

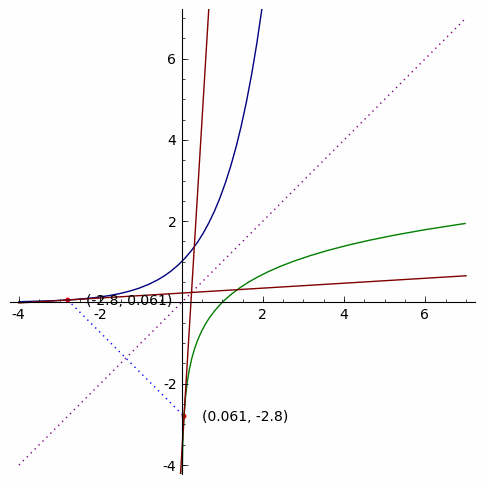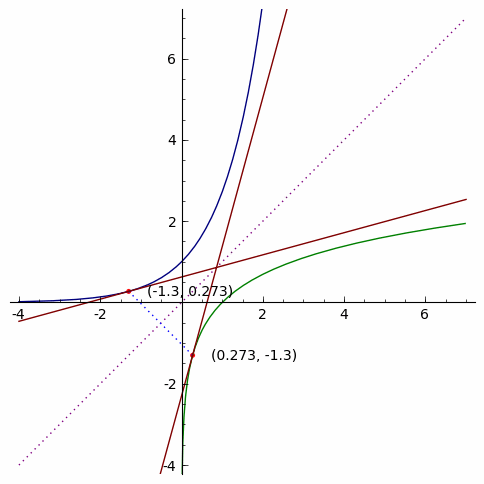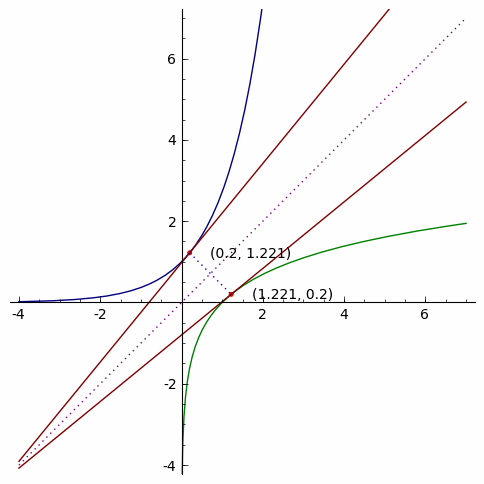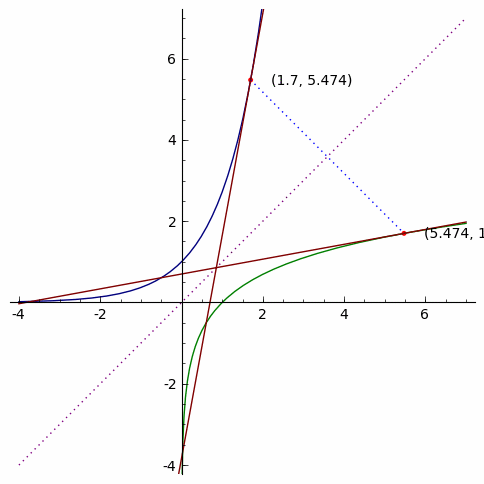
In real analysis (i.e., theory of calculus), this geometrical intuition would then constitute the backbone of what came to be known as the inverse function theorem (on the derivative of an inverse function), which can be proved using the three aforementioned theorems above:

Applications of Inverse Function Theorem

Since differentiable functions and their inverse often occur in pair, one can use the Inverse Function Theorem to determine the derivative of one from the other. In what follows, we’ll illustrate 7 cases of how functions can be differentiated this way — ranging from linear functions all the way to inverse trigonometric functions.

Example 1 — Linear Functions

If we let the original function to be $f(x)=7x-5$, for instance, then, after solving for $x$ and interchanging the $x$ with $f(x)$, we get that $f^{-1}(x) =\frac{x+5}{7}$. In which case, it is clear that $f'(x)=7$ and $[f^{-1}]'(x)=\frac{1}{7}$.

So, this means that we just found out that the derivatives are reciprocal of each other — without appealing to any higher mathematical machinery.

But let’s say that we were to find $[f^{-1}]'(2)$ using Inverse Function Theorem, then here is what we would have to do:

1. Find the correlate of $2$
2. Calculate the derivative of the original function — at this correlate
3. Take the reciprocal

And once that’s done, the number obtained would then be the derivative of the inverse function — at $x=2$.

OK. Let’s see what happens if we follow through the steps:

1. $f^{-1}(2) =\left[ \frac{x+5}{7} \right]_{x=2} = 1$, so the correlate of $2$ is $1$ (i.e., $2$ is to $f^{-1}$ as $1$ is to $f$).
2. $f'(1)=\left[ 7\right]_{x=1} = 7$
3. Taking the reciprocal, we get $\frac{1}{7}$, so that $[f^{-1}]'(2) =\frac{1}{7}$ — as expected from our result before..

Of course. In this case, Inverse Function Theorem is not really necessary, but it does illustrate the mechanics of calculating the derivative of an inverse function fairly well to get the momentum going.

Example 2 — Square Root Function

Now that we know that square and square root functions are inverses of each other (when we restrict the domain of $f(x)=x^2$  to the non-negative numbers), we should be able to calculate the derivative of the square root function with the help of its inverse. To illustrate, here’s how we can find the derivative of $f^{-1}(x)=\sqrt{x}$ at $5$:

1. Correlate of $5$? Just $f^{-1}(5)=\sqrt{5}$. So $5$ is to $f^{-1}(x)=\sqrt{x}$ as $\sqrt{5}$ is to $f(x)=x^2$.
2. Derivative of the original function at $\sqrt{5}$? $f'(\sqrt{5})=\left[ 2x\right]_{x=\sqrt{5}}=2\sqrt{5}$.
3. Reciprocal? $\frac{1}{2\sqrt{5}}$.

Therefore, $(\sqrt{x})'(5)=\frac{1}{2\sqrt{5}}$ — exactly as one would expect from the use of power rule.

So all is good in this case. However, don’t commit the non-mathematician-like mistake of indiscriminately invoking Inverse Function Theorem when the preconditions are not satisfied.

In particular, the derivative of $\sqrt{x}$ does not exist at $x=0$, because derivative of the original function at its correlate is $0$, so that if you choose to take the reciprocal anyway, your derivative will blow up big time. Why? Because the square root function actually has a vertical tangent at $x=0$!

However, when $x>0$, $(\sqrt{x})’=\frac{1}{\left[ 2x\right]_{x=\sqrt{x}}}=\frac{1}{2\sqrt{x}}$, which illustrates that while the derivative of $x^2$ can be proved from definition, the derivative of $\sqrt{x}$ can be proved — with a bit more style — using Inverse Function Theorem!

Example 3 — General Root Functions

While $x^n$ and $\sqrt[n]{x}$ are inverses of each other alright ($n \in \mathbb{N}, n\ge2$), it still needs to be recognized that there are really two kinds of root functions: one where the root is an even (natural) number, and one where the root is odd.

Indeed, when the root is even, $x^n$ and $\sqrt[n]{x}$ are inverses of each other only insofar as the domain of $f(x)=x^n$ is restricted to non-negative numbers, but when the root is odd, these two functions are inverses of each other under the full domain of $f$ (i.e., $\mathbb{R}$).

Using the same steps as before, we can find the derivatives of $f^{-1}(x)=\sqrt[n]{x}$ at $x$ for the appropriate domains:

1. Correlate of $x$: just $f^{-1}(x)$, or $\sqrt[n]{x}$.
2. Derivative of the original function at the correlate: $\left[ nx^{n-1}\right]_{x=\sqrt[n]{x}}=n (\sqrt[n]{x})^{n-1}$
3. Reciprocal: $\frac{1}{n (\sqrt[n]{x})^{n-1}} = \frac{1}{n}\frac{1}{x^{(1-\frac{1}{n})}} = \frac{1}{n}x^{(\frac{1}{n}-1)}$

So for the even root functions, $ (\sqrt[n]{x})’=\frac{1}{n}x^{(\frac{1}{n}-1)}$ for $x>0$, and for the odd root functions, the same is true for $x\ne0$ (why?). Either way, the derivative is left undefined at $x=0$.

For example, $(\sqrt[10]{x})’= \frac{1}{10}x^{\frac{1}{10}-1}$ for $x>0$, and $(\sqrt[3]{x})’=\frac{1}{3}x^{\frac{1}{3}-1}$ for all $x \ne 0$.

And as with before, the formula for the derivative of root functions is really just an special instance of the power rule. In fact, one way to think about it, is that this is how the power rule for derivatives came about — the derivative of $x^n$ proved from definitions, and the derivative of $\sqrt[n]{x}$ proved using Inverse Function Theorem.

Example 4 — Logarithmic functions

Depending on which statements are adopted as definitions, the derivative of logarithmic functions either follows immediately — as a corollary from the definition of logarithm, or is proved using the derivative of its inverse — the exponential function.

Under the natural base $e$, the exponential function $f(x)=e^x$ on $\mathbb{R}$ implicitly defines the logarithmic function $f^{-1}(x)=\ln{x}$ on $\mathbb{R}_+$ (i.e., the set of positive numbers). Using Inverse Function Theorem, the derivative of $\ln{x}$ at any $x>0$ can be calculated as follows:

1. Correlate of $x$: $f^{-1}(x)=\ln{x}$
2. Derivative of the original function at the correlate: $\left[ e^x\right]_{x=\ln{x}} = e^{\ln{x}} = x$
3. Reciprocal: $\frac{1}{x}$

Voila! $(\ln{x})’= \frac{1}{x}$ for $x>0$, as expected.

Wait…what about logarithmic functions of any arbitrary base $b$ ($b>0$, $b \ne 1$)? Well, the change of base theorem for logarithms tells us that:
$$\log_b(x)= \frac{\ln{x}}{\ln{b}}$$
Therefore, for $x>0$:
$$ [\log_b(x)]’ = \left[\frac{\ln{x}}{\ln{b}}\right]’ = \frac{1}{\ln{b}}(\ln{x})’= \frac{1}{x\ln{b}} $$
For example, $[\log_2(x)]’= \left[\frac{\ln{x}}{\ln{2}}\right]’=\frac{1}{x\ln{2}}$, and $[\log_{10}(x)]’=\frac{1}{x\ln{10}}$.

So all is still good. Moving on!

Example 5 — Inverse Trigonometric Function: Arcsine

For an angle $\theta$, $\sin{\theta}$ denotes the y-coordinate of a terminal point with angle $\theta$. For example, $\sin{(-\frac{\pi}{2})}=-1$, $\sin{\frac{\pi}{2}}=1$, and when $\theta$ is between $\frac{-\pi}{2}$ and $\frac{\pi}{2}$, $\sin{\theta}$ is also squeezed between $-1$ and $+1$.

In fact, it’s not too hard to visualize that as $\theta$ moves from $\frac{-\pi}{2}$ to $\frac{\pi}{2}$, $\sin{\theta}$ increases strictly non-stop from $-1$ to $+1$. This means that the function $f(\theta)=\sin{\theta}$ is injective on $I = [\frac{-\pi}{2}, \frac{\pi}{2}]$, and by extension, an inverse function of sine — denoted as $\arcsin(x)$ or $\sin^{-1}(x)$ — can be defined on $f(I) = [-1, 1]$.

Naturally, this leads to a series of calculus-related questions:

1. Where is this inverse sine function differentiable?
2. What is the derivative in that case?

Luckily, this is where Inverse Function Theorem comes to the rescue big time:

1. Correlate of $x$: simply $\sin^{-1}(x)$
2. Derivative of the original function at the correlate: $\left[ \cos{x} \right]_{x=\sin^{-1}(x)}= \cos{(\sin^{-1}(x))}$

OK. Before we move on, let’s simplify the expression a little bit. By Pythagorean Theorem, we know that $\cos^2{\theta}=1 – \sin^2{\theta}$, or that $\cos \theta = \pm \sqrt{1 – \sin^2 \theta}$. In particular:

\[ \cos{\theta}=\sqrt{1 – \sin^2{\theta}} \qquad (\text{if } \cos{\theta}\ge 0) \]

(e.g., if the argument of cosine ranges from $\frac{-\pi}{2}$ to $\frac{\pi}{2}$ (i.e., stays on the right quadrants))

Fortunately, since $\frac{-\pi}{2} \le \sin^{-1}(x) \le \frac{\pi}{2}$ for all $x$ by construction, the aforementioned expression becomes:
$$ \cos{[\sin^{-1}(x)]} = \sqrt{1 – \sin^2[\sin^{-1}(x)]} = \sqrt{1-x^2}$$

All right. That finishes Step 2, which means that when $x=-1$ or $x=-1$, $\sin^{-1}(x)$ is not differentiable as $\sqrt{1-x^2}$ would be $0$. On the other side of the token, it also means that $\sin^{-1}(x)$ would be differentiable anywhere on the interval $(-1,1)$. Let’s finish up the third step in calculating the derivative of inverse sine then:

3. Reciprocal: $\frac{1}{\sqrt{1-x^2}}$

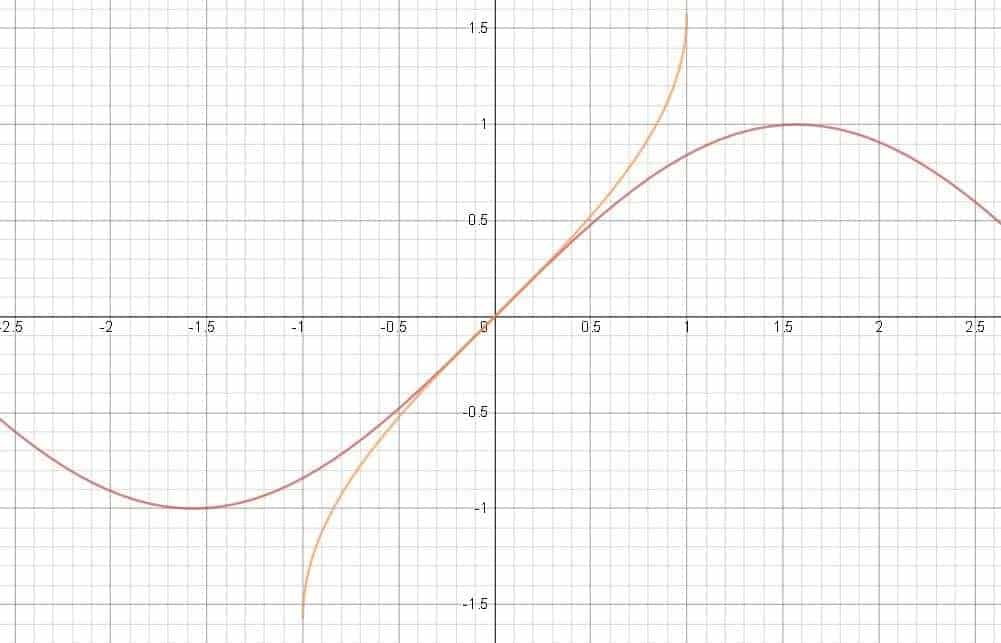
Now, putting everywhere together, we have that $[\sin^{-1}]'(x) = \frac{1}{\sqrt{1-x^2}}$ for $-1<x<1$. This means that while $\sin^{-1}(x)$ is defined and continuous on $[-1,1]$, it is only differentiable on the interval $(-1,1)$.

To be sure, here’s an accompanying graph of $\sin{x}$ and $\arcsin{x}$ — for the record:

Example 6 — Inverse Trigonometric Function: Arccosine

For an angle $\theta$, $\cos{\theta}$ denotes the x-coordinate of a terminal point with angle $\theta$. For example, $\cos{0}=1$, $\cos{\pi}=-1$, and when $\theta$ is between $0$ and $\pi $, $\cos{\theta}$ is also squeezed between $-1$ and $+1$.

Similar to the case with the sine function, it’s not too hard to visualize that as $\theta$ moves from $0$ to $\pi$, $\cos{\theta}$ decreases strictly from $+1$ to $-1$ non-stop. This means that the function $f(\theta) = \cos{\theta}$ is injective on $I = [0,\pi]$, and by extension, an inverse function of cosine — denoted by $\arccos(x)$ or $\cos^{-1}(x)$ — can be defined on $f(I) = [-1, 1]$.

So, as constructed above, when is $\cos^{-1}(x)$ differentiable? And what would the derivative be in that case? Well, to find out more, let’s invoke Inverse Function Theorem again:

1. Correlate of $x$: just $\cos^{-1}(x)$
2. Derivative of the original function at the correlate: $\left[ -\sin{x} \right]_{x=\cos^{-1}(x)} = -\sin{(\cos^{-1}(x))}$

And here’s the fancy Pythagorean trick again! First, $\sin^2{\theta}=1 – \cos^2{\theta}$, so that $\sin \theta = \pm\sqrt{1 – \cos^2{\theta}}$. In particular:

\[ \sin{\theta}=\sqrt{1 – \cos^2{\theta}} \qquad (\text{if } \sin{\theta}\ge 0) \]

(e.g., if the argument of sine ranges from $0$ to $\pi$ (i.e., remains on the upper quadrants))

Luckily, since by construction $\cos^{-1}(x)$ ranges from $0$ to $\pi$, the expression from Step 2 can be simplified as follows:

$$ – \sin{[\cos^{-1}(x)]} = – \sqrt{1 – \cos^2[\cos^{-1}(x)]} = – \sqrt{1-x^2}$$

By inspection, this means that when $x$ is equal to $+1$ or $-1$, $\cos^{-1}(x)$ is not differentiable as $- \sqrt{1-x^2}$ would be $0$. However, the good news is that $\cos^{-1}(x)$ would be differentiable anywhere on $(-1,1)$. Finishing up Step 3, we get that:

3. Reciprocal: $\dfrac{1}{- \sqrt{1-x^2}}$

which shows that $[\cos^{-1}]'(x) = \dfrac{1}{-\sqrt{1-x^2}}$ for $-1<x<1$.

In other words, while arccosine is defined and continuous on $[-1,1]$, it is only differentiable on $(-1,1)$. Similiar to the arcsine function, arccosine also has vertical tangents at $x=-1$ and $x=1$.

And before we move on, let’s just mention that in general, the standard restricted domain for cosine is $[0,\pi]$ when it comes to defining inverse cosine, so that by convention, $\cos^{-1}(x)$ is typically understood to be the inverse cosine function mapping $[-1,1]$ to $[0,\pi]$. Were $\cos^{-1}(x)$ to be defined even slightly differently, the fancy Pythagorean trick introduced earlier could either cease to work out properly — or lead to a new, non-standard formula for the derivative of inverse cosine.

Example 7 — Inverse Trigonometric Functions: Arctangent

GIven an angle $\theta$, $\tan{\theta}$ can be defined as the ratio between the y and x-coordinates of the terminal point with angle $\theta$. Geometrically, $\tan{\theta}$ in essence measures the slope between the origin, and the terminal point with angle $\theta$.

For example, $\tan{0}=0$, because when the angle is $0$, so does the slope. On the other hand, $\tan{\frac{\pi}{4}}=1$, because when the angle is $45^{\circ}$ degrees, the slope is $1$.

In general, we interpret the standard restricted domain of the tangent function to be the interval $(-\frac{\pi}{2}, \frac{\pi}{2})$. Under that interpretation, one can see that the bigger the angle, the more positive the slope. More specifically, as the angle moves from $-\frac{\pi}{2}$ to $\frac{\pi}{2}$, the tangent (i.e., slope) goes from negatively sloppy, flat, to positively sloppy beyond bound.

Algebraically, this means that the function $f(\theta) = \tan{\theta}$ is strictly increasing on $(-\frac{\pi}{2}, \frac{\pi}{2})$ as it travels from $-\infty$ to $+\infty$, making it injective on $I = (-\frac{\pi}{2}, \frac{\pi}{2})$. As a result, a inverse function of $\tan{\theta}$ — usually denoted by $\arctan{x}$ or $\tan^{-1}(x)$ — can be defined on $f(I) = (-\infty,\infty)$.

Hence by construction, $\tan^{-1}(x)$ has this neat property that it is defined everywhere and continuous on $\mathbb{R}$. Interesting! So how does $\tan^{-1}(x)$ behaves in terms of differentiability and derivatives then?

Well, there is one way we can find that out — through Inverse Function Theorem of course!

1. Correlate of $x$: $\tan^{-1}(x)$
2. Derivative of the original function at the correlate: $\left[ \sec^2(x)\right]_{x=\tan^{-1}(x)}=\sec^2(\tan^{-1}(x))$

Now, to prevent us from blindly manipulating symbols, let’s just make sure that things still make sense here. We are talking about the derivative of $\tan^{-1}(x)$, so $x$ could stand for any real number from $-\infty$ to $+\infty$. By construction, $-\frac{\pi}{2} < \tan^{-1}(x) < \frac{\pi}{2}$  (i.e., stays on the right side of the right quadrants). As a result, $\sec^2(\tan^{-1}(x))$ is hence well-defined everywhere on $\mathbb{R}$ — regardless of the value of $x$. Oh well, guess this means that everything is still on track!

Also, since we know that $\sec^2{\theta} = \tan^2{\theta} + 1$ for $-\frac{\pi}{2} < \theta < \frac{\pi}{2}$, the aforementioned expression becomes:

\[ \sec^2(\tan^{-1}(x)) = 1 + \tan^2(\tan^{-1}(x)) = 1 + x^2 \]

which is really good, because $1+x^2 \ge 1 \ne 0$ for all $x \in \mathbb{R}$. This means that the function $\tan^{-1}(x)$ is differentiable everywhere in its domain. Finishing Step 3 quickly yields:

        3. Reciprocal: $\dfrac{1}{1+x^2}$

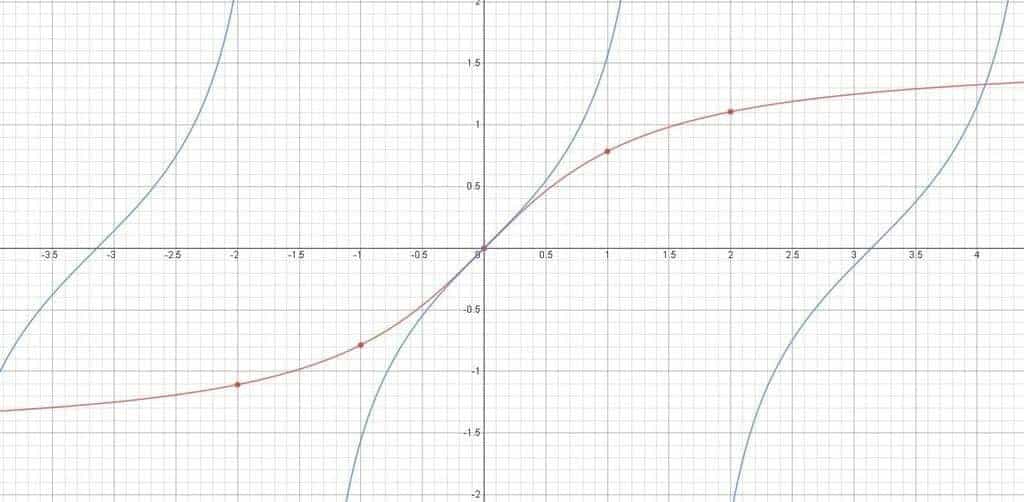
which means that $[\tan^{-1}]'(x) = \dfrac{1}{1+x^2}$ for any $x \in \mathbb{R}$. Perfection!

And to reward ourselves with some “math toys” for the great work being done, here’s a graph of both $\tan{x}$ and $\tan^{-1}(x)$ — as defined using $\tan{x}$’s standard restricted domain:

Closing Words and Beyond

So…is there more to this Inverse Function Theorem thingy? You bet! In particular, here are some recommended functions you might be tempted to differentiate — and add to your own list of favorite derivatives:

• $\sec^{-1}(x)$
• $\csc^{-1}(x)$
• $\cot^{-1}(x)$
• $\sinh^{-1}(x)$ (note: $\sinh{x}= \dfrac{e^x – e^{-x}}{2}$)
• $\ldots$

(heck, why not just construct your own injectively differentiable function from scratch, and find the derivative of its inverse?)

Either way, the take-home lesson — if there is any — is that by acknowledging that some functions come in pairs, and by learning how to maneuver around the formula for the derivative of an inverse, one can double the number of functions in their own table of derivatives, thereby doubling their knowledge on derivatives in general.

And before we go, here is a summary of what we have invented/discovered so far:

OK. Enough of inverse functions for now. Tune in next time for more math goodies perhaps? In the meantime, you can drop by our Facebook and satisfy your craving for more edutaining tidbits and “math cookies“. 🙂

Some Calculus-Related Guides You Might Be Interested In

• Chain Rule for Derivative — The Theory
• Derivatives of $x^x$, $x^{x^x}$…
• Exponent Rule for Derivative: Theory & Applications
• Algebra of Infinite Limits and Polynomial’s End-Behaviors
• Integration Series: The Overshooting Method