
When it comes to quadratic polynomials — which seem to come in all shapes and forms — most of us have spent at least a semester just learning about how to maneuver around them.
Indeed, when we look at a standard math curriculum on quadratic expressions, we would find topics such as square of a sum, square of a difference, completing the square, direct factoring, grouping, difference of squares. AC method (if you’re lucky) and quadratic formula — among others.
In what follows though, we will — in addition to putting some of the aforementioned techniques into good use — develop a general technique for factorising any kind of quadratic polynomials. And yes — the same technique would apply to those with complex numbers as coefficients too!
Table of Contents
Review — Basic Factoring Techniques
When we were in grade school, we were asked to internalize a bunch of rules about factoring polynomials, which include — among others:
- Simple Factoring
- $3x^2+6 = 3(x^2+2)$
- $2x^2 + 4x = 2x (x+2)$
- Perfect Square — Square of a Sum
- $x^2+8x+16= x^2 + 2\cdot x \cdot 4 +4^2 = (x+4)^2$
- $4x^2 + 20x + 25 = (2x)^2 + 2 \cdot 2x \cdot 5 + 5^2 = (2x + 5)^2$
- Perfect Square — Square of a Difference
- $x^2 – 10x + 25 = x^2 – 2 \cdot x \cdot 5 + 5^2 = (x -5)^2$
- $9x^2 – 24x + 16 = (3x)^2 – 2 \cdot 3x \cdot 4 + 4^2 = (3x – 4)^2$
- Difference of Squares
- $x^2 – 5 = x^2 – (\sqrt{5})^2 = (x – \sqrt{5})(x + \sqrt{5})$
- $4x^2 – 9 = (2x)^2 – 3^2 = (2x-3)(2x+3)$
- Completing the Square
- $x^2 + 6x + 7$ $= \underbrace{x^2 + 2 \cdot x \cdot 3 + 3^2} – 3^2 +7 $ $= (x+3)^2 -2$
- \begin{align*} 3x^2 – 6x – 9 = 3(x^2 – 2x – 3) & = 3(\underbrace{x^2 – 2x + 1} – 1 -3) \\ & = 3[(x-1)^2 – 4] \\ & = 3(x-1)^2 – 12 \end{align*}
- Grouping
- $x^2 + 3x + x + 3 = x (x+3) + (x+3) = (x+1)(x+3)$
- $3x^2 + 9x + 2x + 6 = 3x (x+3) + 2 (x+3) = (3x+2)(x+3)$
Of course, these are all very useful techniques, and are all worthy of mastering. The problem with them — if there is any — is that most of them are meant to be used for very special cases only. As a result, the need for better solutions sparks the search for other techniques that are more widely applicable.
Primary Factoring Techniques
When it comes to factoring quadratic polynomials specifically, there are 2 primary techniques that stand out in terms of their general applicability and elegance. These are the Direct Factoring Method, and the AC Method.
Admittedly, while both of these methods are trial-and-error-based heuristics for finding factors with integer coefficients, Direct Factoring requires less steps to carry out (though is more insight-demanding). In contrast, the AC Method takes on a bit more steps, but has a simpler verification process.
Direct Factoring
Just as the name suggests, Direct Factoring consists in finding out the linear factors (i.e., factors of the form $ax+b$) of a quadratic expression directly — mostly through heuristics such as inspection and trial-and-error.
For example, to factorise the trinomial $x^2+13x + 36$ directly, is to find out two linear factors that multiply up to itself:
\begin{equation*}(\Box x + a)(\Box x + b ) = x^2+13x + 36 \end{equation*}
When a trinomial has a leading coefficient of $1$ (i.e., a monic polynomial) — as is in this case — all the $\Box$s reduce to $1$, which simplifies the search a bit:
\begin{equation*}(x + a)(x + b) = x^2+13x + 36 \end{equation*}
To explore a bit, we can expand the left-hand side of the equation, yielding:
\begin{equation*}x^2 + (a+b)x + ab = x^2+13x + 36 \end{equation*}
which suggests that the two constants $a$ and $b$ needs to be such, that they add up to $13$ all of the while multiply up to $36$. After a little bit of experimentation, we see that $4$ and $9$ would do the trick:
\begin{equation*}(x + 4)(x + 9) = x^2 + (4+9)x + 4 \cdot 9 = x^2+13x + 36 \end{equation*}
So Direct Factoring seems to work particularly well with monic polynomials. However, in the general case where the polynomial is not monic, a successful execution of Direct Factoring requires a bit more thinking and ingenuity. Take the case of $3x^2+ 22x+24$ for instance:
\begin{equation*}(\Box x + a)(\Box x + b ) = 3x^2+22x + 24 \end{equation*}
For one, we know that the $\Box$s must be such that they multiply up to $3$. In this case, $3$ and $1$ pop up as obvious factors:
\begin{equation*}(3x + a)(x + b ) = 3x^2+22x + 24 \end{equation*}
The next step then becomes finding out which are the constants $a$ and $b$, such that the left-hand side expands to the right-hand side. By inspection, these constants must multiply up to $24$, leaving us with the following factor pairs: $(1,24)$, $(2,12)$, $(3,8)$, $(4,6)$, $(6,4)$, $(8,3)$, $(12,2)$ and $(24,1)$.
By pure observation again, if $b\ge8$, then there is no way we can get a middle coefficient of $22$ (Why?). But then, that still leaves us with several options. Out of curiosity, let’s try $a=6$ and $b=4$:
\begin{equation*}(3x + 6)(x + 4 ) = 3x^2 + (12+6)x + 24 \ { \color{red} \ne }\ 3x^2+22x + 24 \end{equation*}
OK. This suggests that the middle coefficient (i.e., $18$) is too small. By observation, it seems that boosting the value of $b$ increases the value of the middle coefficient as well. With that in mind, let’s give $a=4$ and $b=6$ a try:
\begin{equation*}(3x + 4)(x + 6 ) = 3x^2 + (18+4)x + 24 = 3x^2+22x + 24 \end{equation*}
Checked! So the numbers work out perfectly in this case.
All right. That pretty much illustrates how in general, factoring a quadratic trinomial directly usually entails making an educated guess first, and adjusting accordingly until the numbers match up. In the cases where the polynomial has well-behaved integer coefficients, this approach is actually not too bad (and could be the fastest even).
AC Method
In some schools out there (e.g., those in British Colombia), a certain factoring technique called the AC Method is taught as the de-facto factoring method — sometimes even with great success.
What is this mysterious AC Method then? Well, it’s essentially a technique for factoring quadratic expressions that is based on splitting the $x$-term into two, resulting in a quadratic expression with four terms — the left two terms being proportional to the right two terms. This proportionality then allows for completing the factoring via Grouping — a basic factoring technique introduced a bit earlier.
More specifically, given a trinomial $ax^2+bx+c$, the AC Method begins by splitting the term $bx$ into two terms (denoted by $b_1x$ and $b_2x$), such that the coefficients $b_1$ and $b_2$ adds up to $b$, but also multiply up to $ac$ — Hence the AC Method.
Once the splitting is done, the resulting quadratic polynomial — $(ax^2 + b_1x) + (b_2x + c)$ — will be such that $ax^2 + b_1x$ is proportional to $b_2x+c$. As a result, Grouping then can be applied to factorise the polynomial with ease.
To illustrate, suppose that we were to factorise $3x^2+22x + 24$ (the same trinomial from the Direct Factoring section) using the AC Method, then we would have to:
- Split the $x$-term: We need to split $22x$ into two terms such that their coefficients add up to $22$ and multiply up to $ac=3(24)=72$. That would suggest the following pairs of coefficients: $(1,72)$, $(2,36)$, $(3,24), \dots , (1,72).$ Obviously, pairs containing numbers such as $24$, $36$ and $72$ are too big to add up to $22$, but with just a bit of thinking, we can see that the pair $(4, 18)$ — or the pair $(18,4)$ — would work out perfectly. Either way, we are warranted to turn $3x^2+22x + 24$ into $3x^2+4x + 18x + 24$.
- Grouping: $(3x^2+4x) + (18x + 24) = x(3x+4) + 6(3x+4) = (x+6)(3x+4)$
So whether it’s by Direct Factoring or AC Method, the result remains the same.
However, as you might notice here, the AC Method is kind of an interesting and elegant technique, in that while for monic trinomials, using direct factoring is faster and almost equivalent to using the AC Method, for non-monic trinomials, the AC Method in effect turns the hard step of figuring out 4 coefficients into an easier step of figuring out 2 coefficients, thereby reducing the complexity of the factoring process — perhaps at the expense of an additional Grouping step, which can be carried out easily with no guesswork involved.
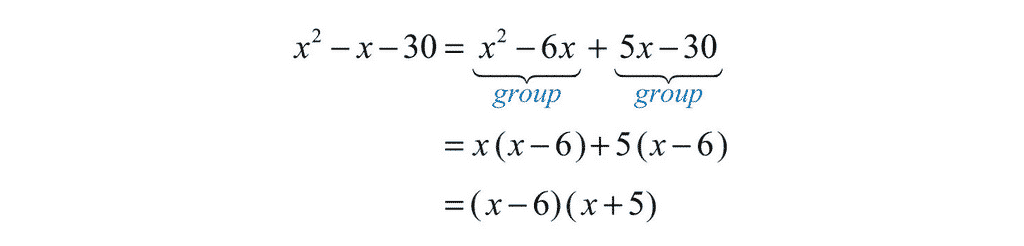
Drawbacks of Primary Factoring Techniques
So… with Direct Factoring and AC Method now in our bag of tricks, we’ve got some pretty powerful tools for factoring quadratic trinomials, don’t we? Well, there is only one problem. Namely, these two techniques don’t work at all — for the vast majority of quadratic trinomials!
OK. How is that possible though? Well, here is why:
And the more you think about it, the more you realise that both Direct Factoring and AC Method are techniques for identifying factors with integer/rational coefficients primarily. As a result, it’s hence no surprise that both methods can fail miserably — for a trinomial that has not been crafted to work out perfectly.
To illustrate, let’s take the trinomial $x^2-x-1$, which is well known to be factorisable with $\frac{1+\sqrt{5}}{2}$ (i.e., the Golden Ratio) as one of its roots. However, if we try to factor it using the primary techniques though, we’ll soon discover that both Direct Factoring and AC Method yields nothing in return.
Actually, this is just the tip of the iceberg. What if we have:
- A trinomial with fractions as coefficients, like $\frac{1}{2}x^2+4x + \frac{3}{5}$? While both Direct Factoring and AC Method work with rational coefficients in theory, we might have a hard time finding out the factors from what seems like an infinite amount of possibilities.
Of course, using some clever tricks, it’s always possible to turn a trinomial of rational coefficients into one with integer coefficients, but hey, the linear factors might still have fractions as coefficients.
Here’s another one, what about:
- A trinomial with irrational coefficients, like $\pi x^2+ 5x + 3$? Again, while Direct Factoring and AC Method can work in theory, you will have a tough time finding the factors from — this time for real — an infinite amount of possibilities (save some special cases, of course!).
So, all this to convey the idea that primary factorisation techniques can fall short in terms of their scope and applicability, and because of that, the search for the ultimate factorisation technique continues…
The General Method — An Introduction
Actually, with the basic and primary factorisation techniques introduced earlier, we already have all the tools needed to factorise any quadratic expressions. All that’s needed really is to put the ingredients together into a coherent algorithm — one that consistently takes care of every issue that got us stuck with the previous methods.
So what is this General Method? In a nutshell, it’s a quadratic-factorisation algorithm based on three key steps — with no guesswork or trial-and-error involved:
General Method — Three Key Steps
- Standardisation: Factor out the leading coefficient, thereby reducing the original trinomial into a monic trinomial.
- Completing the Square: Turning the monic trinomial into the so-called vertex form.
- Factorisation: The vertex form can take on different shapes, but if it is a difference of square itself, then further factorisation is possible; if not, the factorisation is complete by default.
OK. Since an illustration is worth a thousand words, let’s kick off with a few examples before going into full-theory mode.
Case 1: Trinomials With No Root
To factorise a trinomial such as $3x^2+4x+5$ using the ideas behind the General Method, we would kick start with standardisation first:
$$3x^2+4x+5 = 3\left[x^2 + \frac{4}{3}x + \frac{5}{3}\right]$$
Focusing on the monic trinomial, we then proceed to complete the square:
\begin{align*} 3\left[x^2 + \frac{4}{3}x + \frac{5}{3}\right] & = 3\left[\underbrace{x^2 + 2 \cdot x \cdot \frac{2}{3} + \left(\frac{2}{3}\right)^2} – \left(\frac{2}{3}\right)^2 + \frac{5}{3}\right] \\ & = 3\left[ \left(x+\frac{2}{3} \right)^2 \underbrace{- \frac{4}{9} + \frac{15}{9}} \right] \\ & = 3\left[ \left(x-\frac{-2}{3} \right)^2 + \frac{11}{9}\right] \end{align*}
As you can see here, the monic polynomial is now in the form $(x – h)^2 + k$. This is commonly referred to as the vertex form, because we can then deduce that the vertex — or the minimum of the monic polynomial — occurs at $(h,k)$.
With that in mind, we can see that in this case, our monic polynomial has $k=\frac{11}{9}$. This means that if we were to graph this polynomial, then it would start at a height greater than $0$ at the vertex, and increase beyond bound as it moves away from the vertex.
Sure. This can only mean one thing — that the monic polynomial (and by extension, the original trinomial) could not possibly have a root. Here is an accompanying graph of the original trinomial for additional assurance:
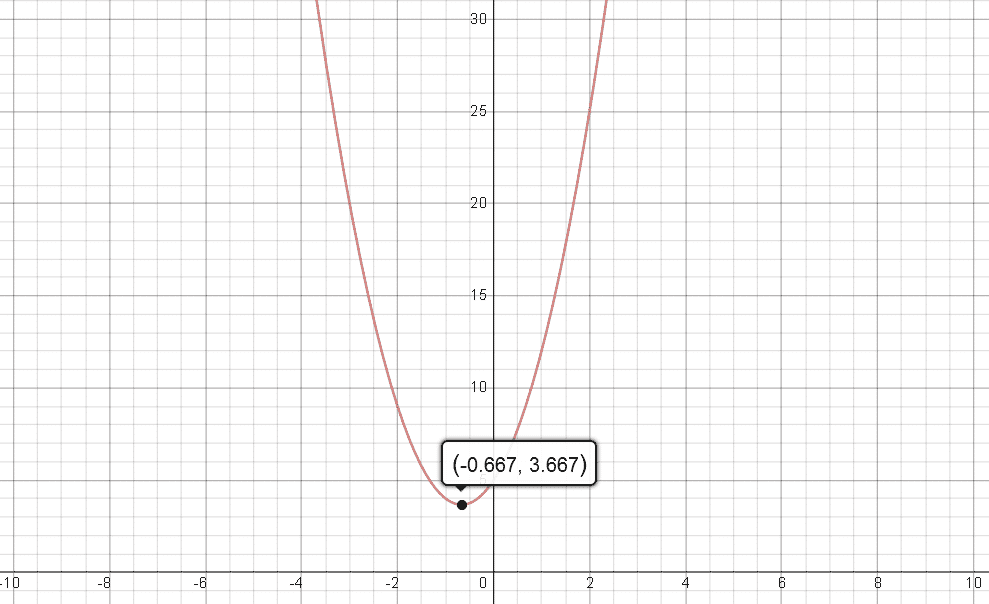
And since the original trinomial has no root, this also means that there is no way that we can factor it either. Why? Because if we could, then the trinomial must have at least a linear factor (i.e., $ax+b$, $a\ne 0$), which means that it actually has a root — namely, $\frac{-b}{a}$!
And with that settled, we can safely dub $ 3x^2 + 4x + 5$ as an irreducible polynomial (i.e., a “prime” polynomial). This is actually in a sense good to know, because we can always leave the trimonial as it is — with its monic polynomial in the vertex form (i.e., $3\left[(x-\frac{-2}{3})^2 + \frac{11}{9}\right]$).
Case 2: Trinomials With Exactly 1 Root
OK. Here’s another one: what about factoring trinomials such as $-2x^2-12x-18$? Well, using the ideas behind the General Method, the following steps are in order:
- Standardise: $-2x^2-12x-18 = -2 [x^2 + 6x + 9]$
- Completing the Square: $-2 [x^2 + 6x + 9] =$ $-2 [ x^2 + 2 \cdot x \cdot 3 + 3^2]=$ $-2 (x+3)^2$ $= -2 [x – (-3)]^2$
- Factorisation: The monic polynomial is in vertex form with $k=0$. Hence the factorisation is complete and no further action is required.
All good. Looking at the vertex form, one can also deduce that $-2x^2-12x-18$ has only a root at $x=-3$, and decreases beyond bound as it moves away from the vertex.
Wow! That was fast isn’t it? Here’s a caveat: cases like these happen quite a bit in textbooks, but very rarely in real-life quadratic models.
Case 3: Trinomials With Exactly 2 Roots
OK. Let’s choose a trinomial we haven’t seen before, say $5x^2 – 16 x + 4$. What could happen if we apply the ideas behind the General Method on this one?
Let’s see… First, standardisng the trinomial, we get that $5x^2 – 16 x + 4$ = $5 \left[ x^2 – \frac{16}{5} x + \frac{4}{5}\right]$.
Second, completing the square on the monic polynomial yields:
\begin{align*}5 \left[ x^2 – \frac{16}{5} x + \frac{4}{5}\right] & = 5 \left[ \underbrace{x^2 – 2 \cdot x \cdot \frac{8}{5} + \left(\frac{8}{5}\right)^2} – \left(\frac{8}{5}\right)^2 + \frac{4}{5}\right] \\ & = 5 \left[ \left(x-\frac{8}{5} \right)^2 \underbrace{- \frac{64}{25} + \frac{20}{25}} \right] \\ & = 5 \left[ \left(x-\frac{8}{5} \right)^2 – \frac{44}{25} \right] \end{align*}
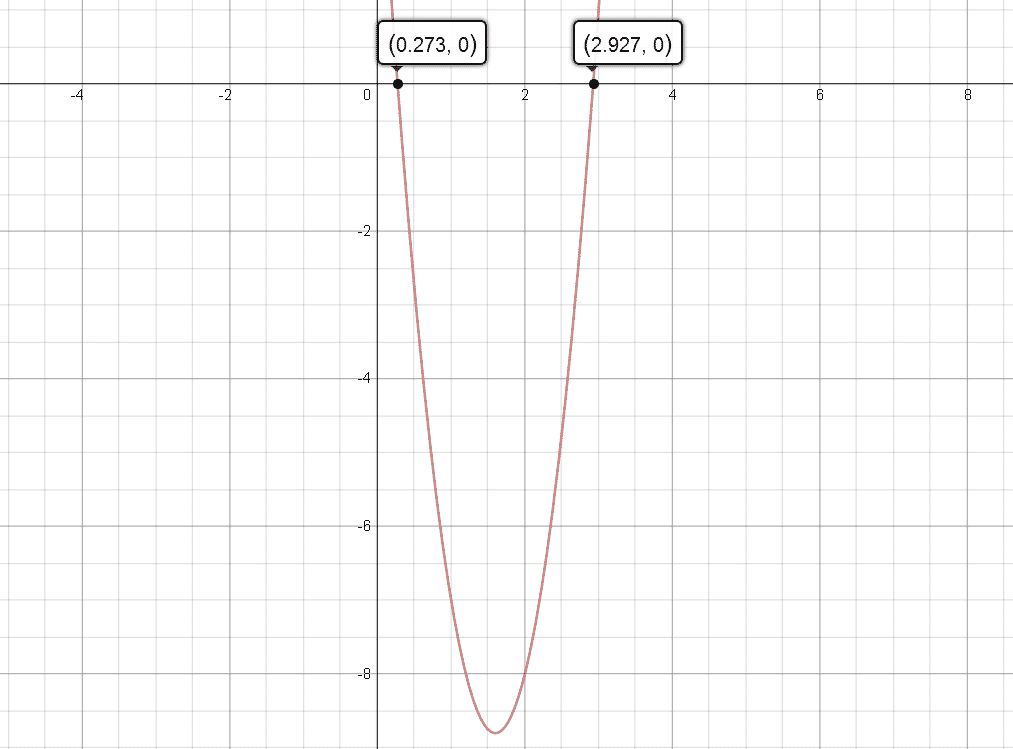
As with usual, the monic polynomial is now in vertex form. However, unlike the other cases, we now have $k=-\frac{44}{25}$ — a negative number.
Actually, this can only be good news, because it means we can apply the difference of square formula to the vertex form!
\begin{align*} 5 \left[ \left(x-\frac{8}{5} \right)^2 – \frac{44}{25} \right] & = 5 \left[ \left(x-\frac{8}{5} \right)^2 – \left(\frac{\sqrt{44}}{5}\right)^2 \right] \\ & = 5 \left[ \left(x-\frac{8}{5} + \frac{\sqrt{44}}{5} \right) \left(x- \frac{8}{5} – \frac{\sqrt{44}}{5} \right) \right] \\ & = 5 \left[ \left(x- \left(\frac{8}{5} – \frac{\sqrt{44}}{5}\right) \right) \left(x- \left(\frac{8}{5} + \frac{\sqrt{44}}{5} \right) \right) \right]\end{align*}
And the factorisation is now complete, revealing the roots of the trinomial $\frac{8}{5}\pm\frac{\sqrt{44}}{5}$. Neat!
The General Method — Theory
Given any trinomial of the form $ax^2+bx+c$ with real numbers as coefficients, the General Method provides a surefire way of completing its factorisation — whenever applicable. To see why, let’s first start by standardising the trinomial:
$$ax^2+bx+c = a \left[x^2+\frac{b}{a}x + \frac{c}{a} \right]$$
Next, completing the square on the monic polynomial yields:
\begin{align*} a \left[x^2+\frac{b}{a}x + \frac{c}{a} \right] & = a \left[\underbrace{x^2+ 2 \cdot x \cdot \frac{b}{2a} + \left(\frac{b}{2a}\right)^2} – \left(\frac{b}{2a}\right)^2 + \frac{c}{a} \right] \\ & = a \left[ \left(x+ \frac{b}{2a}\right)^2 \underbrace{- \frac{b^2}{4a^2} + \frac{4ac}{4a^2}} \right] \\ & = a \left[ \left(x – \frac{-b}{2a}\right)^2 – \frac{b^2 – 4ac}{4a^2} \right] \end{align*}
See that $b^2 – 4ac$ thing? It’s also called the discriminant. For simplicity, we usually denote it by $\Delta$ — the greek letter for Delta.
Furthermore, notice that in the process of completing the square, we also just proved for any quadratic polynomial, the vertex occurs when $x = \frac{-b}{2a}$. In other words, we now know — without having to complete the square again — that the vertex of any quadratic function $f(x)=ax^2+bx+c$ occurs at the point $\left(\frac{-b}{2a}, f(\frac{-b}{2a})\right)$.
And since this $\frac{-b}{2a}$ pops up all the time, we will simply denote it by $h$, so that now we have two shorthands instead of one: $\Delta$ for $b^2 – 4ac$, and $h$ for $\frac{-b}{2a}$.
Under this terminology, the above equation can be simplified as follows:
$$ ax^2+bx+c = a \left[ (x – h)^2 – \frac{\Delta}{4a^2} \right] $$
From this, we see that the monic polynomial is already in vertex form, with $k = – \frac{\Delta}{4a^2} $. Depending on the value of $\Delta$, three possible cases can occur:
Case 1 — $\Delta < 0$: In this case, $k$ — the constant in the vertex form — exceeds $0$. As a result, the polynomial has no root, and hence the factorisation is complete as it is:
$$a \left[ (x – h)^2 – \frac{\Delta}{4a^2} \right]$$
Case 2 — $\Delta = 0$: In this (very lucky) case, $k$ becomes $0$ as well. As a result, the factorisation is also complete and can be simplified as $a (x – h)^2$, with $h$ being the only root.
Case 3 — $\Delta > 0$: In this last case, with $k$ being a negative number, the vertex form can be further factorised using the difference of square formula:
\begin{align*} a \left[ (x – h)^2 – \frac{\Delta}{4a^2} \right] & = a \left[ (x – h)^2 – \left(\sqrt{\frac{\Delta}{4a^2}}\right)^2 \right] & \\ & = a \left[ (x – h)^2 – \left(\frac{\sqrt{\Delta}}{\pm 2a}\right)^2 \right] & \\ & = a \left[ \left(x – h + \frac{\sqrt{\Delta}}{2a} \right) \left(x – h – \frac{\sqrt{\Delta}}{2a} \right) \right] & \\ & = a \left[ \left(x – (h – \frac{\sqrt{\Delta}}{2a}) \right) \left(x – (h + \frac{\sqrt{\Delta}}{2a}) \right) \right] & \end{align*}
Once here, the factorisation is complete, yielding $h \pm \frac{\sqrt{\Delta}}{2a}$ as the two roots of the trinomial. Looking familar? Of course! We just proved the (in)famous Quadratic Formula along the way!
$$ ax^2+bx+c=0 \iff x = \frac{-b}{2a} \pm \frac{\sqrt{\Delta}}{2a} = \frac{-b \pm \sqrt{\Delta}}{2a}$$
OK. Now that we have done all the hard work, we can leverage it into constructing a general algorithm for factoring quadratic expressions, which involves — oddly enough — no factoring at all (at least not in the ordinary sense)!
General Method — The Algorithm
Given a quadratic trinomial with real coefficients (i.e., $ax^2+bx+c$, $a$, $b$, $c \in \mathbb{R}$), the factorisability of the trinomial can be determined using the value of its discriminant $\Delta$, with the factorisation expressible in terms of $\Delta$ and $h$ as follows:
- $\Delta < 0$: The polynomial is irreducible, with the factorisation being $a \left[ (x – h)^2 – \frac{\Delta}{4a^2}\right]$.
- $\Delta = 0$: The polynomial is a perfect square, with the factorisation being simply $a (x – h)^2$.
- $\Delta > 0$: The polynomial has two distinct roots $r_1$ and $r_2$ (shorthands for $h + \frac{\sqrt{\Delta}}{2a}$ and $h – \frac{\sqrt{\Delta}}{2a}$, respectively), with the factorisation being simply $a (x – r_1) (x – r_2)$.
General Method vs. Quadratic Formula
So now you might be asking: “How is this different from the good old Quadratic Formula?” Well, in a nutshell, the General Method is an ultimate technique for factorising quadratic trinomials, while the Quadratic Formula is an ultimate technique for solving their roots.
As a rule of thumb, factorisation generally does much more than simply solving for the roots. And in this case, since the process of factorization also reveals the roots, the General Method can be thought of as a precursor of the Quadratic Formula itself.
In fact, more is true: the General Method also reveals additional information about the quadratic trinomial:
- Vertex: An application of the General Method would reveal the coordinates of the vertex, which determines the position the graph of the trinomial stems from.
- Shape: A factorisation via the General Method reveals the role of the leading coefficient $a$ in determining the orientation (i.e., opens upwards/downwards) and the sloppiness of the graph (of the trinomial).
- Vertex Form: Regardless of whether a trinomial has root or not, the General Method either provides a factorisation for the trinomial, or converts its corresponding monic polynomial into vertex form. While seemingly extraneous, these different representations of trinomials can come in handy in a series of scenarios, where algebraic manipulations are crucial (e.g., partial fraction, trigonometric integrals).
The General Method — Complex Coefficients (Optional)
Taking the ideas behind of the General Method one step further, if a trinomial $ax^2+bx+c$ is such that $a$, $b$ and $c$ are complex numbers (or considered to be to complex numbers), then the above argument with the three cases collapses into one, with the trinomial always factorisable as follows:
$$a \left[ \left(x – (h + \frac{\sqrt{\Delta}}{2a}) \right) \left(x – (h – \frac{\sqrt{\Delta}}{2a}) \right) \right]$$
where $\sqrt{\Delta}$ stands for the complex number on the upper quadrant (i.e., with angle $\theta \in [0. \pi)$) which squares up to $\Delta$.
In this case, we can see that the two roots of the trinomial are $h \pm \frac{\sqrt{\Delta}}{2a}$. so that if we denote these two roots by $r_1$ and $r_2$, the factorisation can be further simplified as follows:
$$ a ( x – r_1) (x – r_2) $$
Not too shabby isn’t it? Incidentally, this also proves in the world of complex numbers, a quadratic polynomial (i.e., a polynomial of degree two) always has two (not necessarily distinct) roots. This is a special case of the so-called Fundamental Theorem of Algebra, which states that in the field of complex numbers, a polynomial of degree $n$ ($n \in \mathbb{N}$) always has $n$ (not necessarily distinct) roots.
This all seems a bit abstract of course, so let’s run through an example to see what how that result comes about. For simplicity, let’s say that we were to factor $3x^2+6x+6$ using the ideas behind the General Method, then we’ll have the following steps:
- Standardise: $3x^2+6x+6=3\left[ x^2 +2x + 2\right]$
- Complete the Square: $3\left[ x^2 +2x + 2\right]=$ $3\left[ (x^2 +2x + 1) +1 \right] =$ $3\left[ (x + 1)^2 +1 \right]$
And here comes the trick: since any non-zero complex number has two roots, we can always turn the vertex form into a difference of square:
\begin{align*} 3\left[ (x + 1)^2 +1 \right] & = 3\left[ (x + 1)^2 – (-1) \right] \\ & = 3\left[ (x + 1)^2 – (\sqrt{-1})^2 \right] \\ & = 3\left[ \left(x + 1 \right)^2 – i^2 \right]\end{align*}
Once there, factorise the difference of square and we’re good to go:
\begin{align*} 3\left[ \left(x + 1 \right)^2 – i^2 \right] & = 3\left[ (x+1+ i)(x+1 – i) \right] \\ & = 3\left[ (x – [-1 – i])(x- [-1 + i]) \right] \end{align*}
This means that while $3x^2+6x+6$ (or equivalently, $3\left[ (x + 1)^2 +1\right]$) is irreducible in the world of real numbers, in the world of complex numbers, it actually factorises to $3\left[ (x – [-1 – i])(x- [-1 + i]) \right]$.
Alternatively, if you prefer factorising $3x^2+6x+6$ using the General Method itself, then here is what you would do:
- We know that for complex numbers, $ax^2+bx+c$ always factorises to $a (x -r_1) (x-r_2)$, with $r_1$ and $r_2$ being $h\pm \frac{\sqrt{\Delta}}{2a}$. Once we gather the ingredients $h$, $\Delta$ and $\frac{\sqrt{\Delta}}{2a}$, we should be all set.
- Since $h \stackrel{def}{=} \frac{-b}{2a}$, we have that $h = \frac{-6}{6} = -1$ in this case.
- Since $\Delta \stackrel{def}{=} b^2 – 4ac$, we get that $\Delta = 6^2 – 4\cdot 3 \cdot 6$ $= -36$.
- Next, $\frac{\sqrt{\Delta}}{2a} = \frac{\sqrt{-36}}{6} = \frac{6\sqrt{-1}}{6} = i$.
Lastly, putting everything together, we get that the roots of the trinomial are $-1 \pm i$, with the factorisation $3 (x – [-1 + i])(x-[-1 – i])$ — same as above.
See the beauty of this? There is no basic/primary factoring techniques involved — just pure computations. 😉 Granted, we did picked an example that’s relatively gentle to work with, but it’s still true that for quadratic trinomials with complex coefficients, whenever we are dealing with $4x^2 + 8x + 9$ or $(2+i)x^2 + \pi x + e+4i$, the General Method takes care of them all!
Afterwords
OK. Now that we have developed the ultimate technique for quadratic factorisation, does it mean that it is over? Well, the search might be, but the need for practices continues on!
To be sure, the fact that the General Method caters to all kinds of quadratic trinomials doesn’t mean that it should be applied all the time. Why? Because unlike the basic and primary factoring techniques, the General Method — while universally applicable — can be quite computationally intensive at times (sometimes even an overkill).
Truth to told, mastering quadratic factorisation is all about learning the mechanics of different kinds of techniques, while adjusting one’s approach accordingly so that a problem can be solved with minimal effort. In this sense, one can even say that quadratic factorisation is as much an art as it is a science — a theme which prevails as one tackles mathematics at a higher level.
$3x^2+6 = 3(x^2+2)$
$x^2+8x+16= x^2 + 2\cdot x \cdot 4 +4^2 = (x+4)^2$
$x^2 – 10x + 25 = x^2 – 2 \cdot x \cdot 5 + 5^2 = (x -5)^2$
$x^2 – 5 = x^2 – (\sqrt{5})^2 = (x – \sqrt{5})(x + \sqrt{5})$
$x^2 + 6x + 7 = \left(x^2 + 2 \cdot x \cdot 3 + 3^2\right) – 3^2 +7 = (x+3)^2 -2$
$x^2 + 3x + x + 3 = x (x+3) + (x+3) = (x+1)(x+3)$
A trial-and-error-based factoring method consisting in finding the coefficients of the two linear factors, so that the linear factors multiply to the quadratic trinomial in question.
For example, in order for $(\Box x + \Box )$ and $(\Box x + \Box )$ to multiply up to $3x^2+22x + 24$, the left $\Box$s should be $3$ and $1$, while the right $\Box$s should be $6$ and $4$.
A trial-and-error-based method for factoring quadratic trinomial, which consists in breaking up the middle term of the trinomial into two, such that the coefficients of these two terms multiply up to $ac$. The resulting polynomial is then factorised via a standard application of Grouping.
For example, $3x^2+22x + 24$ $= 3x^2 + 4x + 18x + 24 = x(3x + $$4) + 6(3x+4) = (x+6) (3x+4).$
For a trinomial $ax^2+bx+c$ with real coefficients, the General Method allows for it to be factorised as follows:
- $\Delta < 0$: The trinomial is irreducible, with the factorisation being $a \left[ (x – h)^2 – \frac{\Delta}{4a^2}\right]$.
- $\Delta = 0$: The trinomial is a perfect square, with the factorisation being simply $a (x – h)^2$.
- $\Delta > 0$: The trinomial has two distinct roots $r_1$ and $r_2$, with the factorisation being $a (x – r_1) (x – r_2)$.
For any trinomial with complex coefficients, the General Method allows for it to be factorised as $a (x – r_1) (x – r_2)$.


You guys are simply amazing! I’ve tried deriving the quadratic roots formula time and again, but never thought of connecting the standard form to the vertex form and seeing what pops out. The General method has also helped improve my intuition for the quadratic trinomials, so thank you guys very much!
I’m going to remember and thank you guys every time I apply one of the many great techniques I’ve learnt here! 🙂
That’s wonderful. Thank you so much!
This is really great. I learned all there is to know about factoring. Perfect level of difficulty and explanation of how it really works. Can you go beyond High School level ? Regards Pat Orlando B.S. Physics Columbia University.
Hi Patrick. Thanks for the kind words. Yes. The vast majority of our guides and eBooks go beyond the high school level, and if we cover a basic topic, that’s usually because there’s a higher-math twist to it!
Good Work on the topic mentioned.
Thank you! We tried to keep the coverage on quadratic factorisation complete (but not too verbose) so that it doesn’t become an algorithmic ritual!
I'm only half way through the article, and I already want to express how helpful it is, how good it is pedagogically: it's very good! Well done, nicely explained.
Hi Andrew. That’s wonderful. Thanks for passing by!
Beautiful tutorial!
Hi Tom. Glad you like it!
I like the way you have factorised the quadratic. Knowing the vertex abscissa is -b/2a, I have taught that the ordinate is -∆/4a which seems quite neat; (-b/2a , -∆/4a)
Hi Scott. Great insight! It’s true that both coordinates can be read from the factorized form of the quadratic as well.